一种具有执行器故障的非线性离散系统的迭代学习控制

李丁巳,杨 轩

(西安工程大学 理学院,陕西 西安 710048)

0 引 言

迭代学习控制(iterative learning control,ILC)是一种智能控制策略,其主要思想是,针对一种在固定时间区间上可重复运行的系统,利用以前的学习信息,逐次更新控制信号,使得在此控制信号支配下,逐步实现系统对目标轨线的精确跟踪[1-5]。与传统的控制方案相比,ILC的优势在于它是基于数据的控制策略,无需知道系统的动力学信息,且便于实现,易于维护[4-5]。因此,其经常应用于模型未知,且对精度要求较高的复杂的工业跟踪控制中。近年来,在基础理论研究及工程实践应用方面,ILC都备受关注。但由于工业控制系统通常在不确定的条件下运行,致使ILC系统会在复杂的环境中出现故障,从而导致控制系统的稳定性和跟踪性能严重下降。此外,ILC的可重复性质,导致其对系统中出现的故障尤为敏感。因此,在设计ILC策略的过程中,容错机制是一个不得不考虑的重要问题。

迭代学习容错控制(ILFTC)是一种新型控制策略。它是针对因器件磨损、卡顿等不确定情况导致系统故障时而不得不考虑的一种控制技术。目前, 对ILFTC控制策略的研究主要集中在批处理工艺方面,如化工、医药生产、现代农业领域等,这主要得益于成熟的二维模型技术。文献[6-9]讨论了这种策略的收敛条件。文献[10-11]针对故障,提出了可靠的迭代学习控制方案。同样,文献[12]利用线性矩阵不等式方法,提出了一种综合迭代学习控制器。在网络化背景下,考虑事件触发传输策略和数据丢失的情况,文献[13]设计了一种满足鲁棒性要求的状态反馈控制器。此外,基于其他技术的ILFTC研究也取得了一定的成果。如为了便于分析故障造成的影响,文献[14]将问题从时域转化为频域,并提出有效的容错策略。文献[15-16]借助模糊理论,提出了基于T-S模糊模型的ILFTC机制。

回顾上述成果不难发现,大多数结论都是在确定故障的情况下得出的。然而,由于实际控制系统经常在不确定的条件下运行,故障的发生具有随机性,难以提前预测。这就导致具有确定性故障的可靠控制器过于保守,以致限制了其实际应用。实际上,在不同周期和不同时间发生故障的事件是相互独立的。主要的挑战是如何制定适当的策略来检测故障,以分析它们对系统瞬态行为的影响。因此,如何根据故障的发生概率设计ILC算法就成为重要的考虑因素之一。 虽然这一课题近年来已有研究[17-18],但仍有一些不足之处有待进一步完善。如被故障影响的控制系统的统计学行为常常被忽视。因此,从统计的角度进一步研究ILC策略的容错能力是一项具有现实意义的工作。这促使笔者在这方面做出突破。

本文主要针对执行器故障的随机性,提出了一种概率意义上的ILFTC算法,当执行器发生随机故障时,首次从统计意义上分析了被控系统的跟踪性能,借助λ范数提出了一个控制策收敛的充分条件,以保证所得结果的实用性。

1 问题描述

考虑如下仿射非线性系统：

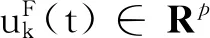
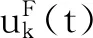
E{αk(t)}=1×P{αk(t)=1}+

需要说明的是,引入随机变量αk(t)的目的是表述执行器错误是否发生。具体地, 如果αk(t)=1,则执行器发生故障;否则,αk(x)=0,则表示执行器不发生故障。 这里0～1 伯努利变量对于任意m≠n,l,s∈Ω,αm(l)与αn(s)相互独立。

因此, 当收到式(2)所示的控制信号时, 受控系统(1)可表示为

令yd(t)(t∈Ω)表示目标轨线, 并定义跟踪误差ek(t)≜yd(t)-yk(t), 在迭代学习控制器内, 控制信号按如下的策略进行更新：

uk+1(t)=uk(t)+Γek(t+1)

(4)

式中：Γ是学习增益矩阵。

注1 本文中执行器故障的机理与文献[17]和[18]不同。在文献[17]和[18]中,执行器故障独立发生在每个学习周期的不同时刻,而不涉及不同学习周期的同一时刻的故障模式。由于ILC的工作模式是可重复性,执行器可能会在每个学习周期中任意时刻随机发生故障。因此,有必要探究在不同的学习周期中同一时刻发生的故障对系统的影响。另外,本文将故障信号分解为乘性故障和加性故障,便于探究故障信号的影响机理,进而分析故障对学习性态的影响,有利于采取必要措施降低故障信号的影响。

为便于理论分析,首先介绍几个基本假设和引理。

假设1 任意给定yd(t)(t∈Ω)存在唯一的控制信号序列ud(t)和一个适当初始状态xd(0)使得动态系统

成立。

假设2 非线性连续函数f(·,·)对任意t∈Ω,满足广义李普希兹条件, 即∀x1,x2∈Rm, 不等式‖f(t,x1)-f(t,x2)‖≤κf‖x1-x2‖成立,其中,κf>0是一个李普希兹常数。

假设3E{xk(0)}=xd(0),∀k∈Z+。

注2 假设1是迭代学习控制问题解的存在性问题。假设2的提出是为了方便后续理论分析。事实上,由于f(·,·)：Rm×p→Rm是一个关于xk(t)的连续可微函数,可以利用f(·,·)：Rm×p→Rm的导数信息确定李普希兹常数κf。在工程实践中,只需知道κf的存在性,而不需要知道其具体值。因此该假设是合理的。假设3是状态可重置条件,它是ILC的基本问题之一[19-21]。 若该条件不能满足,通过ILC策略就无法达到对目标轨线精确跟踪的目的。经典的ILC常常将每次迭代的初始状态设置为xk(0)=xd(0),以达到精确跟踪的目的。然而,该假设与之不同。由于随机发生的执行器故障会降低被控系统的跟踪精度,导致即使每次迭代的初始状态设置为xk(0)=xd(0),也很难达到完全跟踪的目的。于是,在跟踪能达到所需精度要求的前提下,为便于理论分析,退而求其次,将初始状态放宽为假设3。

2 主要结果

定理1 设具有故障的控制信号(2)和控制律(4)应用到满足假设1～3的受控系统(1)。如果学习增益矩阵Γ和故障增益矩阵Ψ(t)满足

则随着迭代次数的增加,系统的输出在Ω上一致跟踪目标轨线yd(t)到其某个邻域内。

证明首先, 引入无故障控制信号误差,有故障控制信号误差和状态误差

由式(6)中第一个方程,并结合式(2)、(4)易知,δuk+1(t)满足如下递归关系：

δuk+1(t)=(I-ΓCBφk(t))δuk(t)-

ΓC(f(xd(t))-f(xk(t)))-

对式(7)两端取范数,并利用假设2,得

‖δuk+1(t)‖≤‖I-ΓCBφk(t)‖‖δuk(t)‖+

这里,

对式(8)两边取期望, 得

E{‖δuk+1(t)‖}≤E{‖I-ΓCBφk(t)‖}

式(9)成立的依据是,随机变量数学期望的保序性[23]。

另一方面,考虑式(6)中的δxk(t),可得

δxk(t)=f(t,xd(t-1))-f(t,xk(t-1))+

Bφk(t-1)δuk(t-1)+

对式(10)两侧取范数,并考虑假设1,得

‖δxk(t)‖≤κf‖δxk(t-1)‖+b‖φk(t-1)‖

对式(11)两侧取数学期望, 可得如下的不等式

E{‖δxk(t)‖}≤κfE{‖δxk(t-1)‖}+

进一步地, 利用递归关系,得

bκfE{‖φk(t-2)‖}E{‖δuk(t-2)‖}+

bE{‖φk(t-1)‖}E{‖δuk(t-1)‖}+

E{‖φk(j)‖}E{‖δuk(j)‖}+

根据假设条件3, 式(13)右侧第一项消失. 因此,有

E{‖φk(j)‖}E{‖δuk(j)‖}+

设φk(t)=diag[φ1,k(t),φ2,k(t),…,φp,k(t)], 其中

φj,k(t)=αk(t)σj(t)+(1-αk(t))=

j=1,2,…,p,于是E{‖φk(t)‖}≤ϖ=max{1,σ1,σ2,…,σp}。从而式(14)可变为

将式(15)代入式(9),得

E{‖δuk+1(t)‖}≤E{‖I-ΓCBφk(t)‖}·

E{‖δuk(j)‖}+φ

(16)

这里,a≫max{1,kf},λ>1是一个充分大的实数。

将式(18)代入式(17),得

(E{‖I-ΓCBφk(t)‖}+

由于对于任意j∈{1,2,…,p},有

‖I-ΓCBφk(t)‖值也具有如下2种不同的情形。

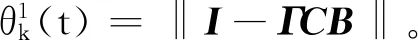
于是,

联立式(19)和(20),得

根据假设条件(5),易知0<ρ<1显然成立。另外, 由于a>>max{1,κf}, 则根据实数的稠密性,必存在一个充分大的数λ,使得

成立。因此,根据式(21)和引理1,有

进而

注3 本文的一个创新点是将执行器故障分解成乘性故障和加性故障。这样处理的好处是可以为寻找消除或减弱故障的方法提供方便。另外,证明过程中, 利用λ范数分析系统的跟踪性能,并导出算法在数学期望意义下收敛的充分条件。实际上,引入a-λt仅仅改变算法的收敛速度,而决定不了算法固有的收敛性态[24]。因此这种分析方法是可行的。

3 数值仿真

考虑如下的非线性系统：

其中,离散的时间区间为Ω={0,1,2,…,20}。

设目标轨线为

假设初始状态满足E{x1,k(0)}=E{x2,k(0)}=x1,d(0)=x2,d(0)=0,初始控制信号为u1,0(t)=u2,0(t)=0, ∀t∈Ω。设学习增益矩阵为

易求,‖I-ΓCB‖=0.772 9。

这种情况旨在说明,在没有任何故障的情况下,对任意给定的一个可达的目标轨线,总可以找到一个最优控制信号,使得在其控制下,系统精确跟踪的目标可以实现。图1为跟踪误差曲线,图2为跟踪性能,其中实线为期望轨迹,虚线为系统经过50次迭代后系统输出曲线。

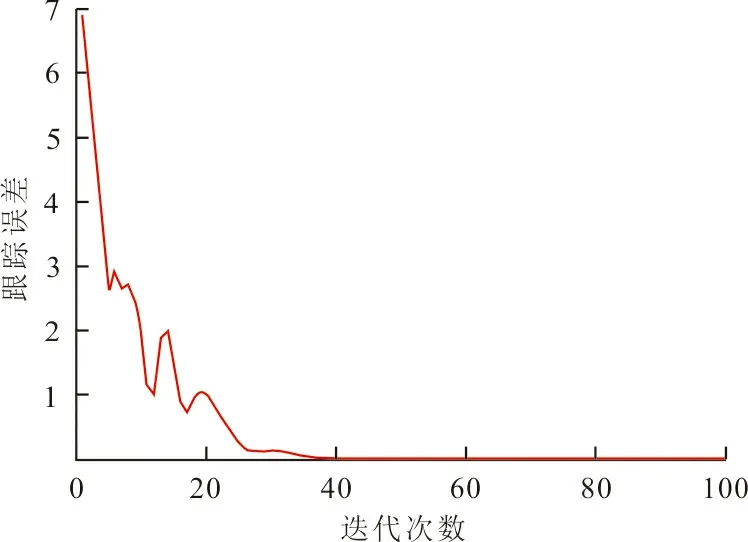
图1 无故障时‖ek(t)‖2曲线 Fig.1 Curve of ‖ek(t)‖2 when fault is absent

(a) y1,k(t)

从图1和图2可以看出,在学习律式(4)的控制下,跟踪误差随着迭代次数的增加在2范数意义下收敛到零,系统(25)的输出可以精确跟踪期望轨迹。这说明在不存在故障的情况下,系统能够准确地跟踪到所期望的轨迹。

Ψ(t)=diag(0.8+0.1sin(ξ(t)t),0.8+

0.1cos(ξ(t)t))

(26)

式中：ξ(t)是一个在(0,1)内变化的随机变量。在这种情况下,‖I-ΓCBΨ(t)‖的取值范围如图3所示。

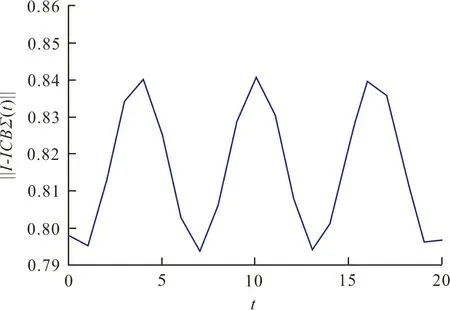
图3 ‖I-ΓCBΨ(t)‖的取值范围Fig.3 Rang of ‖I-ΓCBΨ(t)‖

显然,0.790 0<‖I-ΓCBΨ(t)‖<0.850 0。结合‖I-ΓCB‖=0.772 9,定理1中条件(5)显然成立。

为了验证跟踪误差在数学期望意义下的收敛性态,实验重复了100次,用均值近似表示数学期望。仿真结果如图4、5所示。图4是误差均值曲线,均值误差按计算。其中k是迭代次数,100代表实验次数。

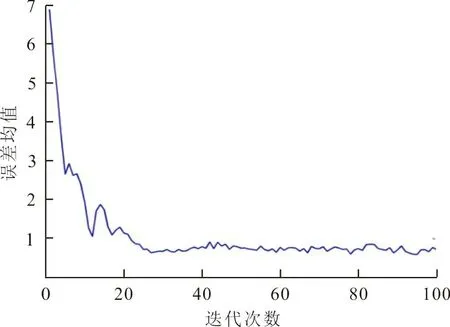
图4 有故障情况下E{‖ek(t)‖2}曲线Fig.4 Curve of E{‖ek(t)‖2} when fault is present

图5是在故障发生概率为5%的情况下,最后一个学习过程中,第50次迭代后系统的跟踪性能曲线。其中,实线是目标轨线,虚线是系统在控制律(2)和(4)控制下的输出轨线。

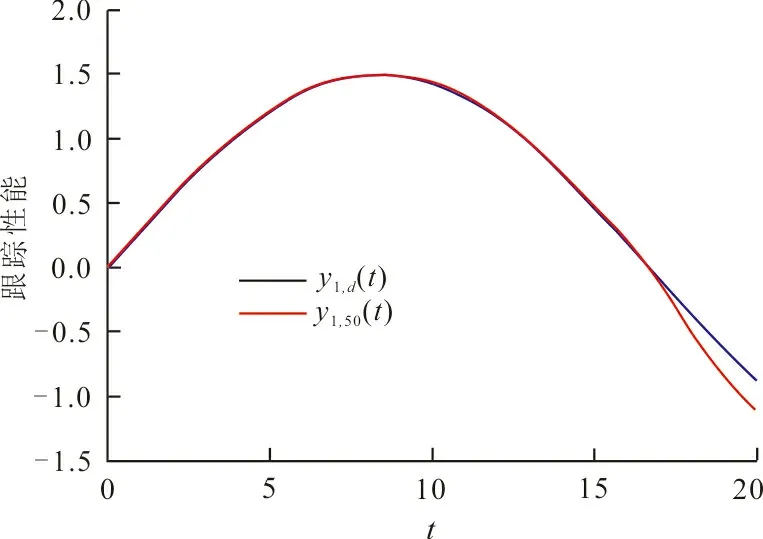
(a) y1,k(t)

由图4可以看出,在学习律(2)和(4)控制下,E{‖ek(t)‖2}最终会收敛到1以下。由图5可以看出,第50次迭代后,系统输出轨线已很接近目标轨线。这表明,虽然发生了故障,但系统输出随着迭代次数的增加,仍能一致跟踪目标轨线到某个邻域内。

4 结 语

本文针对一类执行器随机发生故障的离散仿射非线性系统,当故障满足伯努利分布时,从概率意义上提出了一种迭代学习容错控制策略。该策略的关键是,将执行器故障信号分解为乘性故障信号和加性故障信号。在此基础上,借助λ范数和范数不等式理论,分析了控制策略的学习性态和故障信号对学习性能的影响机理,并导出了控制策略在数学期望意义下收敛的一个充分条件。为了验证所得结果的正确性和有效性,将所提控制策略应用到一个具体非线性系统的跟踪控制中。理论分析和数值仿真结果均表明,当执行器故障以一定的概率发生时,所提策略能够较好地保持系统的跟踪精度。后续研究将在本文基础上,将结论拓展到非仿射非线性系统,并进一步探究故障信号的补偿策略,设计更加有效的控制器。