“调色板上”五彩缤纷的“画”——2016年江苏省无锡市中考第27题赏析与启示

☉江苏省无锡市河埒中学　姜鸿雁

“调色板上”五彩缤纷的“画”——2016年江苏省无锡市中考第27题赏析与启示

☉江苏省无锡市河埒中学姜鸿雁

一、试题呈现及出处

图1

题目如图1，已知▱ABCD的三个顶点A（n，0）、B（m，0）、D（0，2n）（m＞n＞0），作▱ABCD关于直线AD的对称图形AB1C1D.

（1）若m=3，试求四边形CC1B1B的面积S的最大值.

本题是2016年江苏省无锡市中考试题（整份试卷共28题，满分130）第27题，满分10分.

二、试题赏析

1.题面简洁，内涵丰富

题目文字叙述不多，图形线条不繁，用数学独特的简洁魅力，在考生心理上给出了人文关怀.在题面简洁的背后，却包含了丰富的内涵.平面直角坐标系像一块调色板，▱ABCD像一支画笔，在图形翻折的主色调下，“画”出了图形的平移，“画”出了矩形、全等三角形、相似三角形，“画”出了数形结合的韵味，“画”出了从一般到特殊的意境，包含了数量关系上的特殊——最大值，位置关系上的特殊——点B1恰好落在y轴上……了了四十来个字，一幅五彩缤纷的“图画”立刻展示在众人面前，真是简约中蕴藏着丰富的内涵.

2.解法多样，意味深长

本题两小问都不止一种解法，而且对于学生来说，即使不能全部“拿下”，也不至于“无话可说”，给了学生“话语权”.下面笔者谈谈自己解题的大致过程及感悟.

（1）解法一：设BB1交直线AD于E点，如图2，由题意得CB∥C1B1，CB=C1B1，所以四边形CC1B1B是平行四边形，由翻折可知AD垂直平分B1B于E，则▱CC1B1B是矩形.由A、D两点坐标，得则，BB1所以当时，Smax=9.

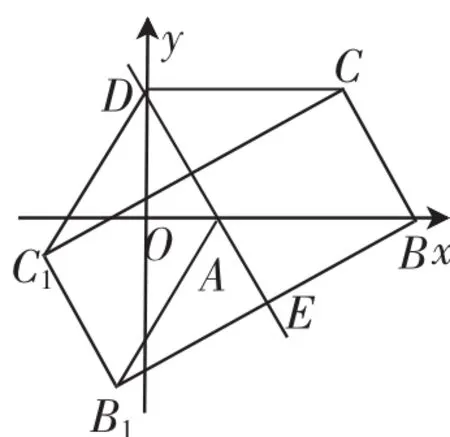
图2

解法二：容易证得△CDC1≌△BAB1，因为S=S▱ABCD+ S▱AB1C1D+S△BAB1-S△CDC1，所以S=2S▱ABCD=4（-n2+3n），以下同解法一.

对于解法一：要求S的最大值，得先对相关图形进行定性分析，配合图形的直观暗示，自然想到确定它的形状，结合翻折、平行四边形、矩形的判定等相关知识，确定四边形CC1B1B的形状是不难的，这一点估计绝大部分学生是能做到的，也就是前面所说的本题给了学生“话语权”.而当确定其形状为矩形后，为计算其面积打开了“一扇窗”，为接下来的定量分析奠定了基础，其中一边长BC很易表示，于是思维聚焦到求BB1的长，进而转化为求BE的长.在学习一次函数及相似三角形时，对“坐标△AOD”在解题过程中发挥的作用，相信不少老师会提醒学生积累相关解题经验；面对相似直角三角形，联想到三角函数，自然是锦上添花，最终利用二次函数求最值将问题解决.综上，对于解法一，不但广泛地考查了初中阶段的重要内容及核心知识点，而且体现思维的自然生长，过程的自然流露.

对于解法二：一切思维的灵感来自于仔细的观察，边看边想、边想边看是重要的学习方式.▱ABCD沿直线AD翻折是显性的已知条件，在并不复杂的图形暗示之下，我们要能想到化旧已知条件为新已知条件的意识，要具备用动态的眼光看静态图形的能力，目光汇聚到△CDC1和△BAB1，图形的平移款款来到眼前，必然会让答题者眼前一亮，足以让人感受到数学的魅力！于是在解决问题的路上多了一条光明大道，简洁的运算过程足以让人兴奋不已！

当然不排除有学生想不到“坐标△AOD”，看不到相似，联系不上三角函数、没有用动态的眼光看静态图形的能力……，但试题能够实现“不同的人在数学上有不同的发展”的目标了.

图3

第（2）问给出的是特殊的位置关系——点B1恰好落在y轴上，必然映射着特殊数量关系，需要揭示的是显性位置关系下隐藏着的隐性数量关系，图3中线段DO、DB1、OB1之间的和差关系或Rt△AOB1中三边之间由勾股定理带来的数量关系都是解决问题的突破口，于是表示线段OB1便成了解决问题的关键.本题相似三角形较多，需要在尝试的过程中不断优化思路.往往思维具有惯性，解法一是受第（1）问的影响，用BE的表达式切换到B1E，再运用△DOA与△DEB1相似，慢慢向“目标”靠近…….解法二则是在众多的相似三角形中，选择了对于解决这个问题最简洁的一对.当然本题一定还有其他解法，笔者全当抛砖引玉.

三、对教学的启示

1.追求自然生长的课堂教学

“生长”是一切有生命的事物的共性，对于学生来说，学习知识的过程、发展思维的过程都是一个个鲜活的自然生长的过程，教师要赋予他们自然生长的权利，提供给他们自然生长的机会.

（1）知识的自然生长.

“知识树”是当下不少老师喜欢将知识以生长的态势展示给学生的外在形态，学生的知识“大树”就在一个个知识“树枝”的生长过程中逐步成长起来的.教师不仅要实现每一块知识学习过程的自然生长，还要有打通各章节知识的能力，使各章节之间实现共通互融.从本题来看，在学习一次函数图像时，常常要研究图像与两坐标轴围成的三角形的周长、面积等问题，既然这个三角形“入镜率”如此之高，我们可以顺水推舟给它命名，不妨叫“坐标三角形”，为后期学习相似三角形，甚至三角函数等知识的自然生长做好铺垫，当相似三角形来到之时，三角函数进入之后，再以平面直角坐标系为“调色板”，给这些知识点能“画出”五彩缤纷的“画”提供了天地.再如，本题呈现的是▱ABCD沿直线AD翻折，而在这一变化中，衍生出三角形的平移、三角形的相似，还有以平面直角坐标系为背景，通过坐标这个视角，量化反映图形变化过程…….本题只是一个“点”，无疑给广大教师一个这样的教学导向：教师要善于打通章节之间的通道，不同章节之间的“营养”会让学生吸收知识更加全面，知识将掌握得更加牢固，“知识树”将生长得更加“茂盛”.

（2）思维的自然生长.

纵观平时课堂教学，基本是教师讲得多，学生听得多，解题教学是如此，初三复习课更是如此.其实，在课堂上，教师给足学生“说话”的时间，让有思路的学生讲思路，会多少讲多少，让不会的学生讲困难在何处，说清在哪里思维受阻，使学生真正参与思考之中，这样的课堂教学才更有效.学生“讲”的过程，便是思维在做“体操”的过程.让学生讲出思路、讲出困惑，分析问题、解决问题的能力在“讲”的过程得到了发展与提升，思维能力才能实现自然生长.假如我们以本题为例，作解题教学的课堂情境：在审题之后，教师可以提出问题：“要求四边形CC1B1B的面积S的最大值，你们觉得如何思考？”如果学生会，让会的学生说思路、讲方法，教师可以追问：“你是怎么想到的？”如果学生不会，教师可以作如下引导，“你的困难在哪里？”“如果我们知道了它的形状，计算它的面积可能应该方便些……”“如何确定它的形状？根据已知条件，我们能得到什么？对确定它的形状有作用么？”“我们还可以从其他动态的视角来审视这幅图形吗？”……而不是直接“灌”它是矩形或各图形面积之间的和差关系.我们认为，“怎么想”远比“怎么做”重要得多.笔者今年没有机会参加阅卷，只能从少部分学生的片言只语中，了解到一些情况.有学生（不算学习困难的学生）反映，不知道如何下手，听了很是奇怪，本题虽不是送分题，但不是难到“不知如何下手”，让不同的学生在数学得到不同的发展”应该是命题者的初衷，但良苦用心却不能得到很好的体现.

反思平时的课堂，常常是教师包办太多，使学生的思维总是处于“被稚化”状态，得不到真正生长，所以一遇到没见过的问题，便束手无策.相反，教师应该做的是：“稚化”自己的思维，让学生的思维成长、强大起来.在课堂上，教师把“讲”的机会更多地让给学生，让“思”的路径本真地流露出来，学生“会想”要远比“会做”重要得多，“会做”不一定“会想”，但“会想”一定“会做”.教师应该长期地给学生提供思维自然生长的“阳光”与“雨露”，只有这样，我们的学生才能在考场上为自己赢得“话语权”.

2.追求揭示本质的课堂教学

数学的运算法则、公理定理、图形结论等都是显性的，怎么在解决问题的过程中，自如地“调度”相关法则定理？这需要我们在提炼数学思想方法的过程中，努力追求揭示问题本质的教学，发展学生的深度思维.揭示问题本质的切入口很多，而本题给了我们两个重要的切入点的启示.

（1）行走在“动静”之间.

在动态问题中，发现“不变”的元素，叫“以静制动”；用动态的眼光看静态的图形，是“用动解静”，在“动”“静”之间思考问题，有助于发现问题的本质.在本题中，问题给出了“▱ABCD沿直线AD翻折变化”是比较明显的“动”，而A、D、B的坐标都是用字母表示的，△CDD1、△BAB1可以看作平移，这些也是“动”的，只是一个比一个来得隐蔽；但D（0，2n），A（n，0）却以坐标的方式“告诉”我们∠ODA的度数不变，除此之外，AD垂直平分BB1，△ODA、△EBA、△OBB1、△EDB1是相似的直角三角形，四边形CD1B1B是矩形，……这些都是不变的，发现“动”与“静”的过程，是思维不断走向深入的过程.

在平时的教学中，我们不能仅仅框于明显的动态问题（比如动点、动直线等问题）才想到“动”，其实“动”与“静”就在我们身边.譬如，在学习正方形、等边三角形、等腰直角三角形、全等三角形、相似三角形……时，教师应该有意识引导学生站在动态的角度，去观察、研究、思考这些“静”态的图形.以图形位似为例，如果两个图形在位似中心的同侧，我们用动态的眼光可以看成是图形在平移的同时进行扩大或缩小（相似）变换，在位似中心异侧时，可以认为图形绕着位似中心旋转180°的同时进行扩大（缩小）变换.再深入下去，图形可以旋转任意角度的同时进行扩大（缩小）变换，也就是通常所说的“旋转相似”；也可翻折的同时扩大（缩小）……教师在平时教学过程，不但要引导学生在“动”中发现“静”的元素，也要练就“静”的图形从“动”的视角看的本领，采用如此辩证的方式思考问题，一定能培养学生的深度思维，有助于把握问题的本质.

（2）穿梭于“数形”之中.

华罗庚先生的“数缺形时少直观，形少数时难入微”已经把“数”与“形”的关系描述得出神入化.不少教师对“数形结合”的认识仅仅停留在数轴、平面直角坐标系、函数图像等这些范畴下，实际上对于一个问题的研究，常是“定性分析”、“定量计算”并驾齐驱，细致分析“形”是“定性分析”的开始，深入计算“数”是“定量计算”的标志.以本题为例，对于第（1）问，确定四边形CD1B1B的形状、研究相关的相似三角形、观察到△CDC1、△BAB1可以看作平移运动，……这些都是对“形”展开思考，而图形面积的计算，二次函数关系式的出现，求出最大值直到问题解决，则是回到“数”的细致计算.在第（2）问，点B1落在y轴上这一特殊的位置关系，必然对应着特殊的数量关系，还是“定性分析”先行，“定量分析”盾后，思维始终在“数形”之间穿梭.在对“形”的深入研究的基础之上，用“数”进行精密计算，沿着“数与形”的微妙关系，我们还可以对这个问题进行如下深入思考：B1点的运动路径是什么（用含m的关系式表示）？如果四边形CD1B1B是正方形时，m、n应该满足怎样的数量关系？……这一系列的过程中，“数”与“形”的对应关系，同时也反映了“一般”与“特殊”的微妙关系，在一般性规律下，给予了特殊的“数量”或“位置”，则一定对应着特殊的“位置”或“数量”关系，我们在透彻研究了“一般”的基础上，深入研究“特殊”的状态，这一切都离不开“数”与“形”的结合！

在日常的教学中，我们对数形结合的理解不能停留在表面，只有教师自身深入研究问题本质，才有可能把学生带向深度思维的海洋.类似“定性与定量”分析，“形与数”的结合，平时解题是屡见不鲜，只要我们有这样的认识问题的视角，引领学生揭示问题的本质也就指日可待了.

如果把课堂比作“调色板”，把“追求自然生长”与“揭示问题本质”比作两支画笔，则教师和学生一起，一定可以用“画笔”勾勒出一幅幅“五彩缤纷”的“画卷”！