基于连续函数为自变量的Bernstein多项式的推广及其曲线曲面应用

孙晓坤， 张 妍

(1.大连理工大学 城市学院 基础教学部，辽宁 大连 116600； 2.辽宁师范大学 数学学院，辽宁 大连 116029)

基于连续函数为自变量的Bernstein多项式的推广及其曲线曲面应用

孙晓坤1， 张 妍2

(1.大连理工大学 城市学院 基础教学部，辽宁 大连 116600； 2.辽宁师范大学 数学学院，辽宁 大连 116029)

用一般的连续函数h(x)替换经典Bernstein基的参变量x,对经典Bernstein多项式进行了推广.通过实例说明，这样得到的Bernstein多项式虽然不一定具有原Bernstein多项式的收敛性，但给出了推广的Bernstein多项式具有收敛性的条件.特别地，当h(x)是折线函数时,推广的Bernstein多项式也可能不具有可导性、保凸性、凸包等性质.而这种推广的Bernstein多项式的优势在于，可以通过调整折线函数的参数值,产生不同于经典形状的曲线和曲面,对自由曲线、曲面的设计具有一定的价值.

Bernstein多项式；折线函数；可导性；保凸性；凸包性质；自由曲线和曲面

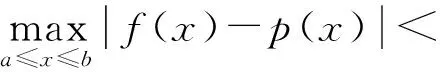
为证明Weierstrass定理,数学家Bernstein构造了一种特殊的多项式[2]:

(1)

式(1)称为f(x)的n次Bernstein多项式,其中，f(x)在闭区间[0,1]上有定义,

(2)

称为Bernstein基函数.

在Weierstrass定理基础上，Bernstein利用式(1)构造性地证明了定理1.

函数的Bernstein多项式简便、精练,容易构造,且当f(x)具有界性、单调不减、凸性等性质时，Bn(f;x)同样具有上述性质，并且还具有可导性、凸包性质等特点[3-4].这使得Bernstein多项式的推广和应用问题成为数值逼近理论的重要研究方面,为自由曲线、曲面设计提供了重要的数学工具[5].

在研究过程中,人们发现如果舍弃了经典Bernstein多项式的诸如可导性、凸性等优越性质，可以得到更广泛的推广和应用.本文就是对Bernstein多项式进行这样一种推广及应用：首先,以[0,1]上的一类连续函数h(x)取代经典Bernstein基函数和多项式中的x,得到推广的Bernstein基函数与多项式,并讨论其性质;其次,讨论h(x)是折线函数时,推广的Bernstein多项式的可导性、凸包、凸性等性质;最后,应用这种推广的Bernstein多项式去生成自由曲线与曲面的形状.

1 推广的Bernstein多项式的性质

考察式(2)中的Bernstein基函数,其中，参变量x可视为函数h(x)≡x.那么,当h(x)≠x时,f(x)的Bernstein多项式Bn(f;h;x)是否仍收敛于f(x)？其次,Bn(f;h;x)的性质与h(x)有什么关系？再次,这类Bernstein多项式有何应用？

在此,要求[0,1]上的函数h(x)满足h(0)=0,h(1)=1.

1.1 推广的Bernstein多项式的收敛性问题

以h(x)替代式(2)中的x得到推广的基函数,记为

(3)

这种基函数相当于对Bv,n(x)作代换x=h(t)(t∈[0,1])得到(仍记参变量为x),因此，Bv,n(h;x)自然保有Bv,n(x)大部分的优越性,如非负性、规范性、对称性等[4].

同理,对式(1)作代换x=h(t)(t∈[0,1]),定义

现抛弃这种变换方法,直接定义Bn(f;h;x)为

(4)

其中，h(x)是[0,1]上的连续函数.

这里以f1(x)=x和f2(x)=x2为例,讨论对应的Bn(f;h;x)的收敛性.

由于

因此

可见当h(x)≠x时,对于任意的f(x)∈C[0,1],{Bn(f;h;x)}不一定收敛于f(x).并且有如下一般性结论：

命题1设f(x)∈C[0,1],Bn(f;h;x)如式(4)所定义,则Bn(f;h;x)收敛于f(x)的充分必要条件是h(x)≡x.

命题2如果f(x)∈C[0,1]是以1,h(x),h2(x),…为基底的函数,则Bn(f;h;x)收敛于f(x).

1.2 h(x)为折线函数时Bernstein多项式的性质

多项式Bn(f;h;x)保有Bn(f;x)的部分性质,如有界性:若f(x)有界,则Bn(f;h;x)有界;单调性:若f(x)和h(x)在[0,1]上单调,则Bn(f;h;x)也单调;但当h(x)表示不同类型的函数时,Bn(f;h;x)的可导性、凸包性质、凸性等性质需单独讨论.下面重点研究h(x)为[0,1]上折线函数时的情形.

(5)

对式(5)求一阶导数,得

图1 Bn(f;h;x)不具凸包性质Fig.1 Bn(f;h;x) without convex hull property

图2 Bn(f;h;x)不具凸性Fig.2 Bn(f;h;x) without convexity

因此,如果h(x)为折线函数,Bn(f;h;x)可能会失去经典Bernstein多项式的诸如可导性、凸包性、凸性等性质,但同时可以创造出更多的自由曲线和曲面的形状,为Bernstein多项式带来更多的应用.

2 h(x)为折线函数时，Bernstein多项式的曲线曲面应用问题

这里选定f(x)=-x2+x+1,x∈[0,1](见图3).此时,经典Bernstein多项式B3(f;x)和B3(f;h;x)分别为

图3 生成函数f(x)=-x2+x+1Fig.3 Generate function f(x)=-x2+x+1

2.1 参数t在(0,)内取值的情形

其图形和经典Bernstein基的参变量x(y=h(x)=x)的图形见图4.

图4 折线函数和y=xFig.4 Polygonal function (x) and y=x

∑1=B3(f;h;x)×B3(f;h;y),

∑2=B3(f;x)×B3(f;y),

图5 t1=时的B3(f;h;x)和B3(f;x)Fig.5 Figures of B3(f;h;x) and B3(f;x) as t1=

曲面Σ1表现出4个小曲面的衔接过渡,比曲面Σ2的形状要复杂得多.

图6 t1=时的曲面Σ1和Σ2的对比Fig.6 Contrast of surface Σ1 and surface Σ2 as t1=

图7 t1=和t2=时的B3(f;h;x)Fig.7 Figures of B3(f;h;x) as t1= and t2=

2.2 参数t在(,1)内取值的情形

讨论方式同t1,生成的曲线B3(f;h;x)见图9,对应的曲面见图10.图9显示t3时曲线改变的方向与t1时相反,这一结果直接影响了曲面Σ1=B3(f;h;x)×B3(f;h;y)的状态.

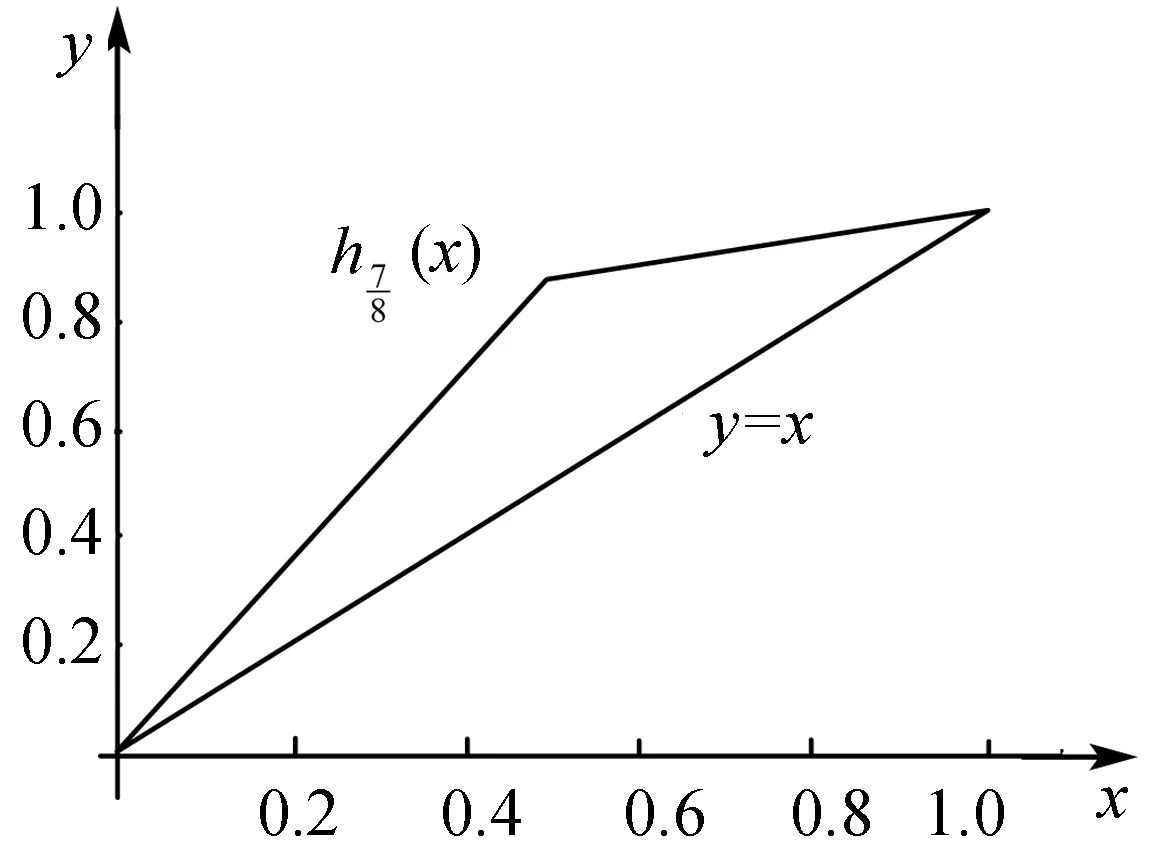
图8 折线函数和y=xFig.8 Polygonal function (x) and y=x

图9 t3=时的B3(f;h;x)和B3(f;x)Fig.9 Figures of B3(f;h;x) and B3(f;x) as t3=

图10 t3=时的曲面Σ1和Σ2Fig.10 Surface Σ1 and Σ2 as t3=

图11 t3=和t4=时的B3(f;h;x)Fig.11 Figures of B3(f;h;x) as t3= and t4=

致谢 本文的撰写得到了辽宁师范大学数学学院王晶昕教授的悉心指导.王教授严谨的治学精神和对研究的精辟见解,使作者受益良多,对作者今后的工作、学习和研究都将产生巨大的影响，在此表示衷心的感谢！

[1] 王仁宏.数值逼近[M].北京：高等教育出版社,1999:1-5.

[2] BERNSTEIN S.Démonstration du théorème de Weierstrass fondée sur le calculdes probabilities[J].Comm Soc Math Khardov,1912,13:1-2.

[3] LORENTZ G G.Bernstein polynomials[M].Toronto:Math Expo Univ of Toronto Press,1953:5-29.

[4] 施法中.计算机辅助几何设计与非均匀有理B样条[M].北京：北京航空航天大学出版社,1994：124.

[5] 王晶昕，王圆圆.Bézier曲线的单侧降阶通近[J].辽宁师范大学学报(自然科学版),2009,32(1):1-3.

GeneralizationofBernsteinpolynomialswithindependentvariableiscontinuousfunctionandapplicationsoffreecurvesandsurfaces

SUNXiaokun1，ZHANGYan2

(1.City Institute， Dalian University of Technology， Dalian 116600, China；2.School of Mathematics， Liaoning Normal University， Dalian 116029, China)

This paper generalizes Bernstein polynomials replacexin classical Bernstein Bases with continuous functionh(x)，however this generalized Bernstein polynomials doesn’t always converge to generating functionf.Especially，ifh(x) is a polygonal function，generalized Bernstein polynomials do not always have differentiability，convexity preserving property and convex hull property，etc.And then，we study curves and surfaces of this generalized Bernstein polynomials by adjusting parameter ofh(x)，etc.

Bernstein polynomials;polygonal function;differentiability;convexity preserving property;convex hull property;free curves and surfaces

O241.5

A

2017-07-20

孙晓坤(1978- )，女，辽宁大连人，大连理工大学副教授．

1000-1735(2017)04-0456-06

10.11679/lsxblk2017040456