一道立体几何中翻折问题的多解剖析

☉苏州市苏州高新区第一中学 宋 涛

立体几何的翻折问题是指将一平面图形翻折后变成空间图形，然后根据平面图形的数量关系、位置关系等来研究空间图形中各元素间的数量关系、位置关系等问题.下面结合实例，将平面图形翻折，变成空间图形，再结合题目条件，来解决空间几何体的空间角（包括异面直线所成的角、线面角、二面角的平面角等）的证明与计算等问题.此类问题往往随着翻折的变化而产生解决问题角度的变化，切入角度多样，方法各异.

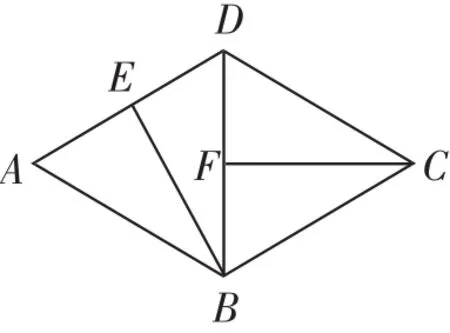
图?

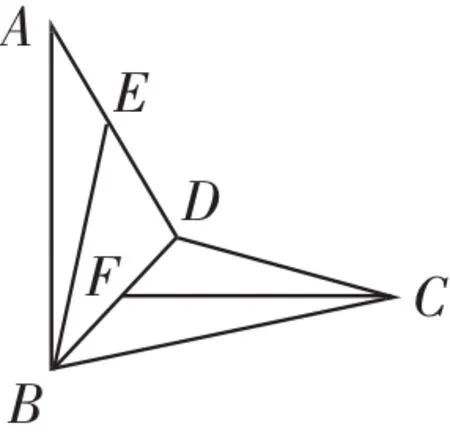
图?

分析：本题涉及立体几何问题的翻折，在翻折过程中，求解相应变量的取值范围问题.注意翻折过程中，有些量是不变的，而有些量是改变的.如何根据翻折的过程来确定异面直线所成的角，可以通过异面直线所成角的定义结合几何性质法、向量法、空间坐标法、极端思维法、特殊模型法等众多的思维方式来处理.

根据异面直线所成角的定义，利用平行线转化为平面角，把空间问题转化为平面问题，利用解三角形来处理与求解.

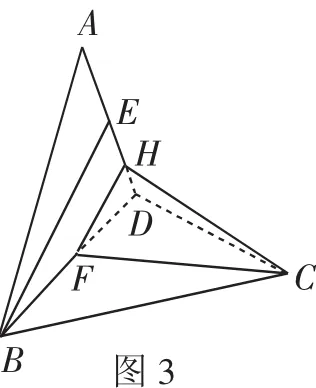
解法1：如图3，过点F作FH∥EB交AD于点H，连接HC.

设菱形ABCD的边长为1，

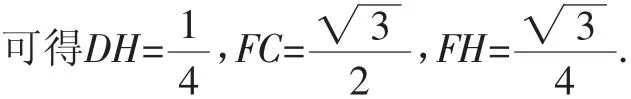
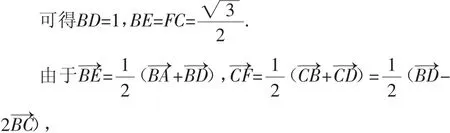
根据平行线的性质可得∠HFC就是异面直线BE与CF所成的角，

分析：根据向量夹角来转化异面直线所成的角，把对应的角转化为向量的夹角问题，利用空间向量的线性运算与数量积来处理与求解，同时注意异面直线所成的角与向量的夹角之间的区别与联系.

解法2：设菱形ABCD的边长为1，

分析：通过建立空间直角坐标系，设出二面角A—BD—C的平面角的大小为θ，从而确定点A的坐标为用空间向量的线性运算与数量积来处理与求解，根据向量的坐标表示求解向量夹角问题，同时注意异面直线所成的角与向量的夹角之间的区别与联系.

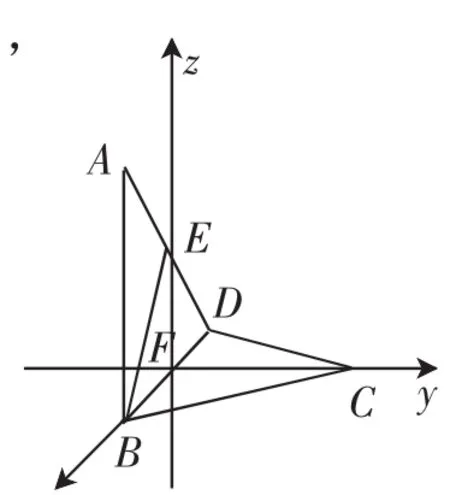
图4

解法3：设菱形ABCD的边长为1

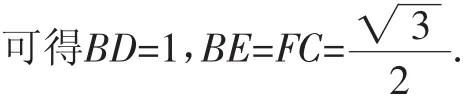
如图4，以F为坐标原点，FB、FC所在直线分别为x轴、y轴建立空间直角坐标系F—xyz，设二面角A—BD—C的平面角的大小为θ（θ∈［0，π］），

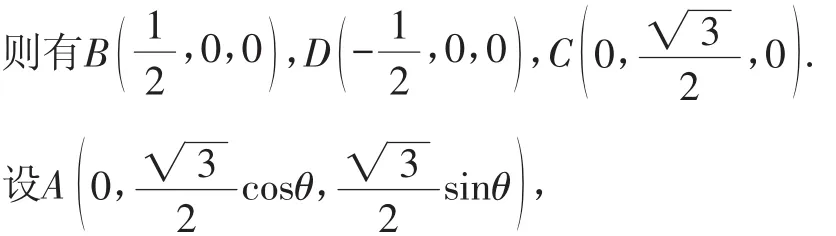
分析：直接通过题目条件判断相应异面直线所成角的大小取值范围的难度比较大，而通过极端思维，根据翻折的极端位置入手，结合翻折时对应的变化带动点的变化所对应的极端位置来分析，可以很快确定答案.

解法4：设二面角A—BD—C的平面角的大小为θ（θ∈［0，π］），异面直线BE与CF所成角为α.

取极端思维：翻折前，几乎没动，此时θ→π，结合平面几何的性质可得此

继续翻折，几乎AD与DC重合，此时θ→0，结合平面几何的性质可得此

分析：先作出辅助线，确定HF与CF所成的夹角就是异面直线BE与CF所成的角，根据翻折时HF所对应的立体几何模型的特征，结合圆锥的性质来确定两直线的夹角问题，从而求解异面直线所成的角.

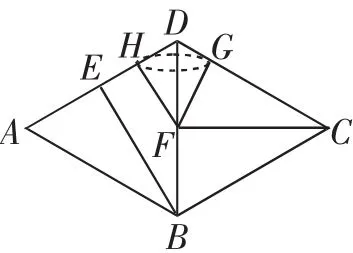
图5

解法5：如图5，过点F作FH∥EB交AD于点H，

根据平行线的性质可得BE∥FH，则HF与CF所成的夹角就是异面直线BE与CF所成的角.

将△ABD沿对角线BD翻折时，HF所对应的轨迹恰好是以HG（G为DC上靠近D点的四等分点）为底面圆直径、DF为对称轴的圆锥的母线，

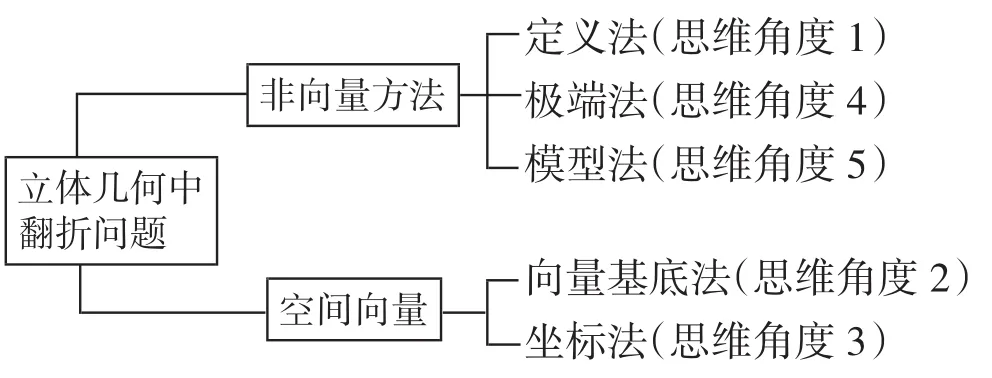
此题是一道立体几何的翻折问题，但从中我们也能体会到立体几何的两个常规思路：非向量方法和向量方法，以此题为例，思考途径如下图：

图?

著名数学家、教育学家G·波利亚说过：“没有任何一个题目是彻底完成了的，总还会有些事情可以做.”通过从多个不同角度来处理，巧妙把该题的底蕴充分挖掘出来，多角度出发，多方面求解，真正体现对数学知识的融会贯通，充分展现知识的交汇与综合，达到提升能力，拓展应用的目的.进而真正达到在学中“悟”，在“悟”中不断提升解题技能.H