EBD(1,2)的参数化动态规划算法改进

李子茂，李　湘

(中南民族大学 计算机科学学院，武汉430074)



EBD(1,2)的参数化动态规划算法改进

李子茂，李湘

(中南民族大学 计算机科学学院，武汉430074)

摘要为了提高Z.Wei和D.Zhu的算法的计算效率，通过引入全局变量Map数组避免重复计算基因家族的邻接关系，将Z.Wei和D.Zhu的固定参数算法的时间复杂度改进为O(s24sn)，空间复杂度保持O(s4sn)；当给定基因组是有向时，适当地修正之后，证明了Z.Wei和D.Zhu的固定参数动态规划算法适合求解有向(1,2)-范例断点距离.相关算法可使用C++来实现，仿真实验进一步验证了改进算法的有效性.

关键词基因组；范例；断点；动态规划

基因组重组问题是近20年来计算生物学领域的研究热点，该问题在生物演化树重建、生物医药技术和发掘生物之间的亲缘关系等方面有重要的应用价值[1].

基因组为基因家族上的基因组成的基因序列，序列上每个基因都是某个基因家族的一次出现，有如下定义：假设X是∑上的一个基因组，如果X中的每个基因g仅出现一次，则称X是平凡的；如果X中的某个基因g至少出现两次，该基因组称为不平凡的[2,3].

断点距离是为了衡量两个基因组的相似度才被引入的概念[2,4].对于不平凡的基因组，D.Sankoff[5]提出范例模型定义两个基因组的断点距离，该模型将不平凡基因组的断点距离计算转换为平凡基因组断点距离计算.给定∑上一个不平凡的基因组G，范例Ex(G)是G的子序列且G中每个基因家族都仅出现一次.∑上两个基因组G1和G2的范例断点距离(简称EBD)即为使得d(Ex(G1),Ex(G2))最小的两个范例的距离.

如果基因组G1中每个基因家族最多出现p次，基因组G2中每个基因家族最多出现q次，G1和G2的范例断点距离称为(p,q)-范例断点距离，记为EBD(p,q).特殊情况下，如果两个基因组存在相同的范例，则其范例断点距离为0，称该问题就是零-范例断点距离问题，简称ZEBD(p,q).

D.Sankoff为解决EBD(p,q)提出了一个分支定界算法[5].C.Nguyen等人随后对EBD(p,q)提出了分而治之的方法，并开发了一个结合分而治之和分支定界技术的程序[6]，该程序通过使用细菌的基因序列作为输入数据验证了有效性.

在问题的计算难度上，D.Bryant首次证明EBD(1,2)是NP-hard[7]，Z.Chen,B.Fu和B.Zhu证明ZEBD(3,3)是NP-hard[8].2010年，G.Blin,G.Fertin,F.Sikora和S.Vialette证明ZEBD(2,2)也是NP-hard，如果p≥2,q≥2，EBD(p,q)也是NP-hard的，而且在多项式时间内任何性能比都不能近似EBD(p,q)[3].S.Angibaud等人证明EBD(1,2)是APX-hard[4]，L.Bulteau和M.Jiang证明使用多种距离度量很难近似EBD(1,2)[9].

考虑到固定参数计算的棘手性，B.Zhu证明FPT算法不能有效解决EBD(2,2)[10].近年来，许多算法被提出，如G.Blin等人通过颜色编码技术[11]为ZEBD设计时间复杂度O(n2n)的算法[3]，他们也针对ZEBD给出了一个时间复杂度O(n22ss3)的参数化算法，其中n是输入基因组的长度，s是基因家族的最大跨度.B.Fu和L.Zhang[12]针对EBD(1,q)给出了一个时间复杂度为O(2nmo(1))的算法，M.Jiang证明ZEBD(1,q)能在多项式时间内被解决[13].D.Zhu和L.Wang[14]针对ZEBD(2,2)提出了一个时间复杂度为O(n21.86121n)的算法.其他一些EBD算法可见文[2,7,15,16].

EBD(1,2)是最基础的范例断点距离问题，该问题是APX-hard，但却鲜有算法对该问题进行求解.Z.Wei和D.Zhu[17,18]提出固定参数算法动态规划算法解决EBD(1,2)，时间复杂度和空间复杂度分别为O(s4sn2)和O(s4sn)，其中n是基因家族的数量，s是基因家族的最大跨度.令G=G[1]……G[m]是∑上的一个串.为了方便，我们用G[i,j]代表G[i]……G[j]的连续子序列，i≤j.对于j≥i来说，在G中G[i]和G[j](注意G[j]=G[i])的跨度是j-i.一个串的跨度是在这个串中所有基因家族的最大跨度.实际上，在基因组中，基因家族的跨度都很小[19].

本文使用全局变量改进Z.Wei和D.Zhu[17,18]的固定参数算法计算两个基因组间范例断点距离的时间复杂度，同时修订该算法使之适合求解有向不平凡基因组的范例断点距离.

1无向EBD(1,2)参数化动态规划算法

对无向不平凡基因组G2=G2[1],G2[2],G2[3],…,G2[m]，每个∑中基因家族在G2中最多出现两次，如果G2[1,i-1]中没有包含与G2[i]相同的基因，则基因G2[i](1≤i≤m)在G2中是第一次出现；否则，基因G2[i](1≤i≤m)在G2中第二次出现.

这里简要介绍文献[17，18]提出的无向基因组EBD(1,2)动态规划算法并对算法时间复杂度进行改进，首先定义下述符号概念如表1.

表1EBD(1,2)的动态规划算法中涉及符号的含义

Tab.1The meaning of symbols in dynamic programming algorithm of EBD(1, 2)

符号含义基因家族集合X上的串G1上平凡的基因组G2上不平凡的基因组Ex(X)X的范例集合EX相对于G1的最小范例E1X中的任意范例d(G1,E)E与G1的断点个数x某个基因X·xX右边连接基因xXxX中剔除基因x|X|X的长度,即X中的基因个数Φ上平凡串的一个集合T(Φ,s)Φ的s-terminal集合MΦ的最小s-kernelMK(Φ)返回Φ的最小s-kernel的子程序KEx[i-1]Ex(G2[1,i-1])的最小s-kernelmin(KEx)KEx中找到最小范例的子程序

对表1作补充说明：d(G1,E)=min{d(G1,E1)|E1∈Ex(X)}为G1和X的范例断点距离.若X=X[1],X[2],…,X[k]，则X的长度为k，如果k>t,称X[k-t,k]为X的t-终端，记为t-terminal；如果k≤t，则X本身是X的t-terminal.T(Φ,s)={E1[|E1|-s,|E1|]︱E1∈Φ}.如果Φ的一个子集与Φ有相同的s-terminal集合，称该子集为Φ的一个s-内核，记为s-kernel，基数为|T(Φ,s)|.M={E2∈Φ︱d(G1,E2)≤d(G1,E1),E1[|E1|-s,|E1|]=E2[|E2|-s,|E2|]，E1∈Φ}，如果|M|=|T(Φ,s)|，那么M是Φ的最小s-kernel.

1.1动态规划算法找到最小范例

如果G2[1,i]的两个或两个以上的范例有相同的s-terminal，则相对于G1而言它们中存在一个最终成长为G2的最小范例[17].如果用哈希表存储Φ中的串，则在时间复杂度O(k·|Φ|)内找到Φ的最小s-kernel.

引理1Ex(G2[1,i])的最小s-kernel肯定包含G2[1,i]相对于G1而言的最小范例，s为G2的跨度[17].

由引理1可知，通过递归计算Ex(G2[1,i])(1≤i≤m)的最小s-kernel能得到Ex(G2)的最小s-kernel.

定理1当1≤i≤m，令KEx[i-1]是Ex(G2[1,i-1])的最小s-kernel，那么Ex(G2[1,i])的最小s-kernelKEx[i]能用如下方法递归计算[17]：

(1) 当i=1时，KEx[i]={G2[1]}；

(2) 当i≥2时，基因家族G2[i]在G2中第一次出现，KEx[i]=MK(KEx[i-1]·G2[i])；

(3) 当i≥2时，基因家族G2[i]在G2中第二次出现，且G2[i]出现在G2[1,i-1]中，KEx[i]=MK(KEx[i-1]∪((KEx[i-1]G2[i])·G2[i])).

由定理1可知，相对于G1而言，KEx[i]肯定是Ex(G2[1,i])的最小s-kernel.该算法的时间复杂度取决于KEx[i]的基数.动态规划算法Exemplar(G1,G2)可以在Ex(G2[1,m])即Ex(G2)中找到最小范例，其中MK和min(KEx)含义参照表1，算法描述如下：

Algorithm Exemplar(G1,G2)

Input:∑={1,2,3,…,n}上平凡基因组G1和不平凡基因组G2

Output:相对于G1而言，G2的最小范例

i=1时，KEx={G2[1]};

fori=2 tomdo

ifG2[i]是第一次出现

KEx=MK(KEx·G2[i]);

else

KEx=MK(KEx∪((KExG2[i])·G2[i]))

end if

end for

return min(KEx)

1.2优化算法的时间复杂度

由引理1和定理1可知，如果Ex(G2[1,i])的两个或多个范例有相同的s-terminal，那么这些范例当中最多有一个范例能在KEx[i]中，因此，KEx[i]的s-terminal集合中串的数目足够来估算KEx[i]中串的数目.如果KEx[i]中串的长度最多是s，也就是说最多有s个基因家族出现在G2[1,i]中.因为每个基因家族在G2中最多出现两次，KEx[i]最多有2s个串.如果KEx[i]中串的长度至少是s+1，则KEx[i]最多有4s个串，有如下引理2.

引理2Ex(G2[1,i])的最小s-kernel最多有4s个串[17].

计算Ex(G2[1,i])的最小s-kernel的运行时间是整个算法的时间复杂度基础，注意KEx[i]是Ex(G2[1,i])的最小s-kernel.为方便起见，我们把在KEx[i-1]中的任意一个范例E表示为E=E[1],E[2],…,E[k].

(1)如果基因家族G2[i]在G2中是第一次出现，由引理2可知，KEx[i-1]·G2[i]最多有4s个串.在Z.Wei和D.Zhu的算法中，其计算基因组断点函数每次都需要使用O(n)时间计算基因组G1的逆函数Map，即每个基因家族的所在位置数组，从而每次在判断E[k]·G2[i]相对G1而言是断点或相邻时需要O(n)时间(E·G2[i]断点数为E的断点数或E的断点数加1，这取决于E[k]·G2[i]是断点还是邻接).我们发现只需经过一次基因组G1的逆函数Map计算并将之保存为全局变量，就可以在O(1)的时间来确定E[k]·G2[i]相对G1而言是断点或是相邻.

更进一步，假设所有KEx[i-1]范例集已经被确定，则Z.Wei和D.Zhu花O(4sn)的时间确定KEx[i-1]·G2[i]串中的范例集，而我们只需花O(4s)时间，使用哈希表来保存KEx[i-1]·G2[i]中的串时，能在O(s4s)时间下找到KEx[i-1]·G2[i]的最小s-kernel.因为长度为s+1的一个串被当做是哈希表的关键值，在KEx[i-1]·G2[i]中串设置哈希表会花O(s4s)时间，这些哈希表占用的空间为O(s4sn).

(2)如果基因家族G2[i]在G2中是第二次出现，则G2[i]出现在G2[1,i-1]中，由引理2可知，(KEx[i-1]G2[i])·G2[i]最多有4s个串.设E′=(EG2[i])·G2[i]，E与G1的断点数目为d(E,G1)，在Z.Wei和D.Zhu的算法中，同样其计算基因组断点函数每次都需要使用O(n)时间计算基因组G1的逆函数Map，需用O(n+s)时间计算出(EG2[i])·G2[i]相对G1的断点个数.我们发现同样只需经过一次基因组G1的逆函数Map计算并将之保存为全局变量，就可以在O(1)的时间来确定E[k]·G2[i]相对G1而言是断点或是相邻，计算E′相对于G1断点数目可以通过计算E′[k-s,k]和E[k-s,k]的断点数目得到，时间复杂度为O(s)，从而Z.Wei和D.Zhu花O(4sn)的时间确定KEx[i-1]·G2[i]串中的范例集，而我们只需花O(s4s)时间，使用哈希表来保存(KEx[i-1]G2[i])·G2[i]中的串时，能在O(s24s)时间下找到(KEx[i-1]G2[i])·G2[i]的最小s-kernel.

考虑到算法的循环次数不超过2n次，整个算法的时间复杂度不超过O(s24sn).

定理2优化Exemplar(G1,G2)算法总能在O(s24sn)时间和O(s4sn)空间下返回Ex(G2)的一个最小范例.

1.3仿真实验

我们使用C++语言实现了Exemplar(G1,G2)及其优化算法，使用Visual C++ 6.0的编译环境在Intel(R) Core(TM) i7-4790 CPU @3.60GHz 4GB Memory个人计算机上运行算法.在实验中记录Exemplar(G1,G2) 的运行时间，算法平均运行时间结果如图1和图2所示.通过随机基因组的仿真对比实验表明，我们优化后的算法能在1200 s内处理5000个基因家族，G2重复率为70%，跨度分别为6和10的两个基因组断点距离的计算，比Z. Wei和D. Zhu的算法更加高效.无向EBD(1, 2)实例的两个基因组G1和G2测试数据产生方法见文[17].

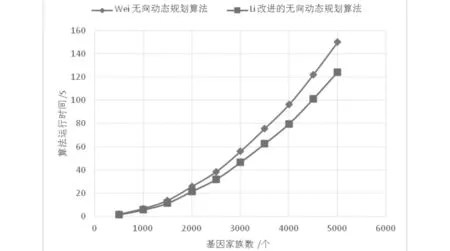
图1　计算n个基因家族G1和G2的范例断点距离的运行时间，跨度为6，G2中重复基因家族的概率为70%Fig.1　The running time for computing the exemplar breakpoint distance of G1and G2with n gene families,where the nontrivial gene families of G2are bounded by 70%, and the span of G2is 6

图2　计算n个基因家族G1和G2的范例断点距离的运行时间，跨度为10，G2中重复基因家族的概率为70%Fig.2　The running time for computing the exemplar breakpoint distance of G1and G2with n gene families,where the nontrivial gene families of G2are bounded by 70%, and the span of G2is 10

2有向EBD(1,2)参数化动态规划算法

给定∑={1,2,3,…,n}上平凡有向基因组G1=G1[1],G1[2],G1[3],…,G1[n]和不平凡有向基因组G2=G2[1],G2[2],G2[3],…,G2[n]，其中Gi[j]=k或Gi[j]= -k，k∈∑，i= 1,2, 1≤j≤n.一个在∑中基因家族在G2中最多出现两次，如果G2[1,i-1]中没有包含与|G2[i]|相同的基因，则基因家族|G2[i]|( 1≤i≤m)在G2中是第一次出现；否则，基因家族|G2[i]|(1≤i≤m)在G2中第二次出现.在G2中G2[i]和G2[j](注意|G2[j]|=|G2[i]|)的跨度是j-i，一个串的跨度是在这个串中所有基因家族的最大跨度.这里我们将无向基因组EBD(1,2)求解推广到有向基因组.有向基因组邻接和断点概念见Sankoff[5]提出的范例模型.以下运用动态规划算法找到最小范例.

引理3E是G2[1,i-1]的一个范例.如果基因家族|G2[i]|在G2中是第一次出现，那么E·G2[i]是G2[1,i]的一个范例[17].

引理4E是G2[1,i-1]的一个范例.如果|G2[i]|家族在G2中是第二次出现，那么G2[i]出现在E中或-G2[i]出现在E中.第一种情况，G2[i]出现在E中，那么E和(EG2[i])·G2[i]都是G2[1,i]的范例；第二种情况，-G2[i]出现在E中，那么E和(E-G2[i])·G2[i]都是G2[1,i]的范例.

引理5令E1和E2是G2[1,i-1]的两个范例，E1和E2最少有s+1个基因.基因家族|G2[i]|在G2中是第一次出现.如果E1和E2有相同的s-terminal，同时d(E1,G1)≤d(E2,G1)，那么E1·G2[i]和E2·G2[i]有相同的s-terminal，并且d(E1·G2[i],G1)≤d(E2·G2[i],G1)[17].

科思创中国区总裁盛秉勇（Bjoern Skogum）表示：“可持续发展是科思创的核心战略支柱之一，中国正对化工行业进行大规模整治重组，以实现可持续发展。在这一背景下成为行业榜样意义重大。作为一家跨国企业，科思创将继续为中国化工行业的可持续发展作贡献，到2025年将生产每吨产品产生的二氧化碳排放较2005年降低50%，利用我们全球化的专业知识让中国更美好。”

引理6令E1和E2是G2[1,i-1]的两个范例，E1和E2最少有s+1个基因，而且基因家族|G2[i]|在G2中是第二次出现.如果E1和E2有相同的s-terminal，而且d(E1,G1)≤d(E2,G1)，这里有两种情况，第一种情况，G2[i]出现在E1和E2中，那么(E1G2[i]·G2[i]和(E2G2[i])·G2[i]有相同的s-terminal，而且d((E1G2[i])·G2[i],G1)≤d((E2G2[i])·G2[i],G1)；第二种情况，-G2[i]出现在E1和E2中，那么(E1-G2[i])·G2[i]和(E2-G2[i])·G2[i]有相同的s-terminal，而且d((E1-G2[i])·G2[i],G1)≤d((E2-G2[i])·G2[i],G1).

证明第一种情况和第二种情况本质是相同的.我们不妨证明第二种情况.令E1=E1[1],E1[2],…,E1[k],E2=E2[1],E2[2],…,E2[k],E1′=(E1-G2[i])·G2[i],E2′=(E2-G2[i])·G2[i].因为基因家族|G2[i]|在G2中是第二次出现，而且跨度是s，那么-G2[i]必定在E1[k-s,k]和E2[k-s,k]中.因为E1[k-s,k]=E2[k-s,k]，那么(E1[k-s,k]-G2[i])·G2[i]=(E2[k-s,k]-G2[i])·G2[i]，也就是E1′[k-s,k]=E2′[k-s,k].因为G2[i]的跨度是s，-G2[i]≠E1[k-s]，-G2[i]≠E2[k-s].那么d(E1′,G1)=d(E1,G1)-d(E1[k-s],G1)+d(E1′[k-s,k],G1)和d(E2′,G1)=d(E2,G1)-d(E2[k-s],G1)+d(E2′[k-s,k],G1).因为d(E1,G1)≤d(E2,G1)，那么d(E1′,G1)≤d(E2′,G1).

引理7Ex(G2[1,i])的最小s-kernel肯定包含G2[1,i]相对于G1而言的最小范例[17].

定理3当1≤i≤m，令KEx[i-1]是Ex(G2[1,i-1])的最小s-kernel，那么Ex(G2[1,i])的最小s-kernelKEx[i]能用如下方法递归计算：

(1)当i=1时，KEx[i]={G2[1]}；

(2)当i≥2时，基因家族|G2[i]|在G2中第一次出现，KEx[i]=MK(KEx[i-1]·G2[i])；

(3)当i≥2时，基因家族|G2[i]|在G2中第二次出现，且G2[i]出现在G2[1,i-1]中，KEx[i]=MK(KEx[i-1]∪((KEx[i-1]G2[i])·G2[i]))；

(4)当i≥2时，基因家族|G2[i]|在G2中第二次出现，且-G2[i]出现在G2[1,i-1]中，KEx[i]=MK(KEx[i-1]∪((KEx[i-1]-G2[i])·G2[i])).

证明当i=1时，KEx[i]={G2[1]}是显而易见的.当i≥2时，有以下两种情况.

(a) 如果基因家族|G2[i]|在G2中第一次出现，由引理3可知，G2[1,i]的每个范例都在Ex(G2[1,i-1])·G2[i]中.因为KEx[i-1]是Ex(G2[1,i-1])的s-kernel，每个在Ex(G2[1,i-1]·G2[i])串都对应于一个在KEx[i-1]·G2[i]的串，这些对应的串都有相同的s-terminal.也就是说，MK(KEx[i-1]·G2[i])肯定是Ex(G2[1,i-1])的s-kernel.对于任意一个范例E，E∈Ex(G2[1,i-1])，令E′是在KEx[i-1]中的范例，而且与E有相同的s-terminal.因为KEx[i-1]是Ex(G2[1,i-1])的最小s-kernel，d(E′,G1)≤d(E,G1).由引理5可知，E′·G2[i]与E·G2[i]有相同的s-terminal，而且d(E′·G2[i],G1)≤d(E·G2[i],G1).也就是说，MK(KEx[i-1]·G2[i])肯定是Ex(G2[1,i-1])的最小s-kernel.

(b) 如果基因家族|G2[i]|在G2中第二次出现，也就是说可能G2[i]出现在G2[1,i-1]中，可能-G2[i]出现在G2[1,i-1]中，这两种情况肯定有一种情况发生.不妨假设-G2[i]出现在G2[1,i-1]中.由引理4可知，G2[1,i]的每个范例肯定在Ex(G2[1,i-1])和(Ex(G2[1,i-1])-G2[i])·G2[i]并集中.因为KEx[i-1]是Ex(G2[1,i-1])的s-kernel.对于一个在Ex(G2[1,i])中的串，肯定在KEx[i-1]或(KEx[i-1]-G2[i])·G2[i]中有一个串和它对应，这两个串有相同的s-terminal.令E是Ex(G2[1,i-1])中任意一个范例，令E′是在KEx[i-1]中的范例，而且与E有相同的s-terminal.因为KEx[i-1]是Ex(G2[1,i-1])的最小s-kernel，d(E′,G1)≤d(E,G1).由引理7可知，E′和(E′-G2[i])·G2[i]都是G2[1,i]的范例.由引理6可知，(E′-G2[i])·G2[i]与(E-G2[i])·G2[i]有相同的s-terminal，而且d((E′-G2[i])·G2[i],G1)≤d((E-G2[i])·G2[i],G1).总结一下，MK(KEx[i-1]∪((KEx[i-1]-G2[i])·G2[i]))肯定是返回Ex(G2[1,i])的一个最小s-kernel.同理可得，如果G2[i]出现在G2[1,i-1]，MK(KEx[i-1]∪((KEx[i-1]G2[i])·G2[i]))肯定是返回Ex(G2[1,i])的一个最小s-kernel.

由定理3知，Z.Wei和D.Zhu的固定参数化算法可以用来解决有向基因组EBD(1,2).相对于G1而言，有向动态规划算法可以在Ex(G2[1,m])即Ex(G2)中找到最小范例.这个算法称为SignedExemplar(G1,G2)，其中MK和min(KEx)含义参照表1，算法描述如下.

Algorithm SignedExemplar(G1,G2)

Input:∑={1,2,3,…,n}上平凡有向基因组G1和不平凡有向基因组，其中Gi[j]=k或Gi[j]=

-k，k∈∑，i=1,2,1≤j≤n.

Output:相对于G1而言，G2的最小范例

当i=1时，KEx={G2[1]};

fori=2 tomdo

if |G2[i]|是第一次出现

KEx=MK(KEx·G2[i]);

else

ifG2[i]出现在G2[1,i-1]中

KEx=MK(KEx∪((KExG2[i])·G2[i]))

else-G2[i]出现在G2[1,i-1]中

KEx=MK(KEx∪((KEx-G2[i])·G2[i]))

end if

end if

end for

return min(KEx)

3结语

Z.Wei和D.Zhu的固定参数化动态规划算法可解决无向EBD(1,2)，我们优化了该算法的时间复杂度，通过对比试验，验证了我们算法的高效性.当给定基因序列是有向时，通过适当地修正，我们证明Z.Wei和D.Zhu的固定参数动态规划算法适合求解有向(1,2)-范例断点距离.因为没有遇到任何一个EBD(1,2)实例有O(4s)个s-kernel范例集，所以固定参数化算法是否能给出一个更好的复杂度分析有重要的意义.

参考文献

[1]LiZM,WangLS.ZhangKZ.Algorithmicapproachesforgenomerearrangement:areview[J].IEEETransactionsonSystems,Man,andCybernetics,PartC(ApplicationandReviews),2006,36(5): 636-648.

[2]BlinG,ChauveC,FertinG,etal.Comparinggenomeswithduplications:acomputationalcomplexitypointofview[J].IEEE/ACMTransanctionsonComputationalBiologyandBioinformatics,2010,4(4):523-534.

[3]BlinG,FertinG,SikoraF,etal.Theexemplarbreakpointdistancefornontrivialgenomescannotbeapproximted[M].Heidelberg:Springer,2009:357-368.

[4]AngibaudS,FertinG,RusuI,etal.Ontheapproximabilityofcomparinggenomeswithduplicatess[J].JournalofGraphAlgorithmsandApplications,2009,13(1): 19-53.

[5]SankoffD.Genomerearrangementwithgenefamilies[J].Bioinformatics,1999,15(11): 909-917.

[6]NguyenCT,TayYC,ZhangL.Divide-and-conquerapproachfortheexemplarbreakpointdistance[J].Bioinformatics,2005,21(10):2171-2176.

[7]BryantD.Thecomplexityofcalculatingexemplardistances[M].Berlin:SpringerNetherlands,2000:207-211.

[8]ChenZ,FuB,ZhuB.Theapproximabilityoftheexemplarbreakpointdistanceproblem[M].Heidelberg:Springer,2006: 291-302.

[9]BulteauL,JiangM.Inapproximabilityof(1,2)-exemplardistance[J].IEEE/ACMTransactionsonComputationalBiology&Bioinformatics,2012,10(6):1384-1390.

[10]ZhuB.Approximabilityandfixed-parametertractabilityfortheexemplargenomicdistanceproblems[C]//ZhuBinhai.TheoryandApplicationsofModelsofComputation.Heidelberg:Springer,2009:71-80.

[11]AlonN,YusterR,ZwickU.Colorcoding[J].JournaloftheACM,1995,42(4): 844-856.

[12]FuB,ZhangL.Apolynomialalgebramethodforcomputingexemplarbreakpointdistance[C]//FuBin,ZhangLouxin.BioinformaticsResearchandApplications.Heidelberg:Springer,2011:297-305.

[13]JiangM.Thezeroexemplardistanceproblem[J].JournalofComputationalBiology,2011,18(9): 1077-1086.

[14]ZhuDM,WangLS.Anexactalgorithmforthezeroexemplarbreakpointdistanceproblem[J].IEEE/ACMTransanctionsonComputationalBiologyandBioinformatics,2013,10(6): 1469-1477.

[15]AngibaudS,FertinG,RusuI,etal.Efficienttoolsforcomputingthenumberofbreakpointsandthenumberofadjacenciesbetweentwogenomeswithduplicategenes[J].JournalofComputationalBiology,2008,15(8):1093-1115.

[16]BonizzoniP,VedovaGD,DondiR,etal.Exemplarlongestcommonsubsequence[J].IEEE/ACMTransactionsonComputationalBiologyandBioinformatics,2007,4(4): 535-543.

[17]WeiZX,ZhuDM,WangLS.Aparameterizedalgorithmfor(1,2)-exemplarbreakpointdistance[C]//IEEE.2014IEEEInternationalConferenceonBioinformaticsandBiomedicine(BIBM).Washington:IEEEComputerSociety,2014:11-16.

[18]WeiZX,ZhuDM.Adynamicprogrammingalgorithmforunsigned(1,2)-exemplarbreakpointdistanceproblemwithspanconstraint[C]//IEEE.2013SixthInternationalConferenceonBusinessIntelligenceandFinancialEngineering.Washington:IEEEComputerSociety,2013:39-43.

[19]ShiG,ZhangL,JiangT.MSOAR2.0:Incorporatingtandemduplicationsintoorthologassignmentbasedongenomerearrangement[J].BMCBioinformatics,2010,11(1):1-14.

AnImprovedParameterizedDynamicProgrammingAlgorithmfor(1,2)-ExemplarBreakpointDistance

Li Zimao, Li Xiang

(CollegeofComputerScience,South-CentralUniversityforNationalities,Wuhan430074,China)

AbstractInordertoimprovethecomputationalefficiencyofZ.WeiandD.Zhu′salgorithm,thispaperimprovesthetimecomplexityofZ.WeiandD.Zhu′salgorithmtoO(s24sn)byintroducinganglobalarrayMaptoavoidrepeatedlycomputingoftheadjacenciesofgenefamilies,whilethespacecomplexitykeepsO(s4sn).Ifthegivengenomesissigned,weshowthatZ.WeiandD.Zhu′sfixedparameterdynamicprogrammingalgorithmissuitabletocomputethesigned(1, 2)-exemplarbreakpointdistanceafterminorrevision.ThealgorithmsareimplementedbyusingC++language,andsimulationsindicatetheproposedalgorithms′effectiveness.

Keywordsgenome;exemplar;breakpoint;dynamicprogramming

收稿日期2016-03-18

作者简介李子茂(1974-)，男，副教授，博士，研究方向：算法设计与分析、计算复杂性，E-mail：3030207@mail.scuec.edu.cn

基金项目湖北省自然科学基金资助项目(61379059)

中图分类号TP312

文献标识码A

文章编号1672-4321(2016)02-0116-06