向量在二面角等相关问题中的应用

潘朝毅，马玉雯

（成都师范学院 数学学院，成都 611130）

同济版高等数学教材[1]将两平面的夹角θ 定义为两平面的法线向量n1与n2所夹的锐角（或直角），. 但在立体几何中的二面角φ 要么与θ 相等，要么为θ 的补角，因此需要先行观察去判断该二面角是钝角还是锐角，才能在前面求出θ 的基础上确定φ 值. 在很多二面角相关问题中，仅靠观察是无法确定到底是钝角还是锐角，这种观察的方法严格讲也是不严谨的. 而要不加入人工观察，则需进一步限定所讨论的二面角内的两个平面法向量n1与n2的方向为“一进一出”，这时就唯一确定了

利用确定向量积方向的右手法则，选取两个平面法向量n1与n2的方向为“一进一出”很容易. 本文将利用空间向量的线性运算及混合积、向量积的运算规律及性质，给出其在二面角相关问题的若干应用.

1 已知两平面π1 与π2 所构成的二面角内有点M0，求该二面角的角度φ

设平面πi方程为Aix + Biy + Ciz + Di= 0，则法向量ni={ Ai,Bi,Ci}，同时记Mi( xi,yi,zi)为平面πi中的任一点，i = 1,2. 将M0( x0,y0,z0)坐标代入πi方程左端得

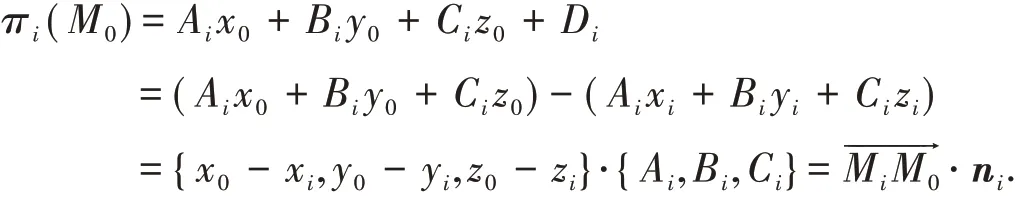
由于M0( x0,y0,z0) 是二面角内的点，故πi( M0) ≠0，而平面πi的法向量ni方向对此二面角当πi( M0) ＞0 时为“进入”，当πi( M0) ＜0 时为“出离”. 故此得到结论：

将M0( x0,y0,z0) 坐标分别代入两平面方程左端计算，若两值异号，则二面角的角度

解析几何教材[2]中规定平面π 的法式方程为xcosα + ycosβ + zcosγ - p = 0 时，特别要求p 非负，本质上就是确保n0={ cosα,cosβ,cosγ } 为从原点指向平面π 的单位法向量，此即通过πi( M0) ＜0 来保证ni={ Ai,Bi,Ci}是从点M0( x0,y0,z0)指向平面πi的法向量的特例.

2 用向量工具证明三面角余弦定理

三面角余弦定理在求解某些二面角问题时有独特优势[3]. 利用向量的混合积运算性质和双重向量积公式，可以很简洁地证明该定理.

引理1a ⋅( b × c )= ( a × b )⋅c

引理2( a × b )× c = ( a ⋅c ) b - ( b ⋅c ) a

定理1（三面角余弦定理）四面体（三棱锥）O - ABC 中，记∠AOC = α,∠BOC = β,∠AOB = γ,二面角A - OC - B = φ，则

证明：记的单位向量为a,b,c，则∠( a,c )= α，∠( b,c )= β，∠( a,b )= γ. 注意到若取平面AOC 的法向量为a × c，平面BOC 的法向量为b × c，这两个方向对于二面角A - OC - B 一定为“一进一出”，由于

故cosγ = cosαcosβ + sinαsinβcosφ.

3 空间已知两点M1 与M2 所在平面发生折叠后，求两点的距离

设空间某平面π 上两点M1( x1,y1,z1) 与M2( x2,y2,z2) 在π 上一条直线L 的两侧，沿直线，这里( x0,y0,z0) 是直线L 上一点M0的坐标，{ cosα,cosβ,cosγ )是直线L 的单位方向向量v0的坐标，为点M1,M2折叠后的新位置. 下面我们利用向量工具推导出计算折叠后两点间距离d()的公式.

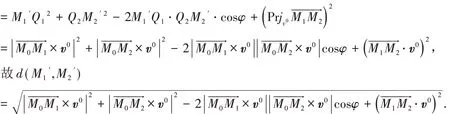
如果考虑点M1与M2及直线L 在平面直角坐标系xoy 的特殊情形，即已知坐标M1( x1,y1)与M2( x2,y2)及直线方程Ax + By + C = 0，那么直线的单位方向向量，若记f ( Mi)= Axi+ Byi+ C，i = 1,2. 注意到M1与M2在直线L 两侧，所以f ( M1) f ( M2) ＜0，因此

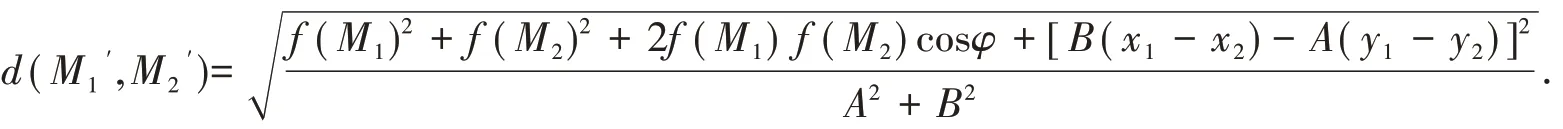
上式与文献[4]导出的结果一致，对比可知用向量工具推导更为直接，应用范围也更广.

4 对角线向量定理与对棱角公式的统一证明

二面角问题的一个常见背景就是空间四面体. 四面体的六条边中任意两条之间的夹角余弦可通过计算对应两向量的数量积求出，而任意两边对应向量的数量积均可由另外四边的平方和与差表出，这就是在文献[5]中被称作的对角线向量定理与对棱角公式.

定理2 在四边形ABCD 中，两条对角线向量的数量积

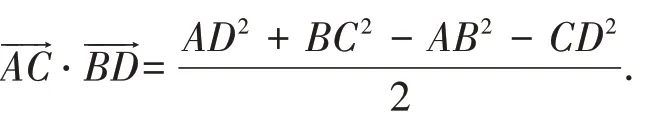
定理3 在四边形ABCD 中，两条对边（棱）向量的数量积

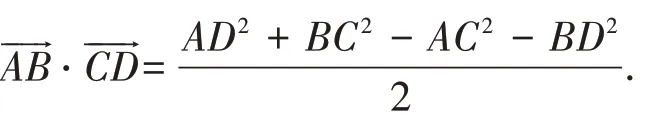
文献[5]对这两个定理在平面四边形的情形分别给出了证明，同时指出在空间四面体（三棱锥）中结果也成立. 该文献通过运用这两个定理演示求解了多例立体几何问题. 对于复杂的立体图形包括动态翻折问题，将向量运算直接化为简单的线段长度计算，要求的几何量非常明确，极少依赖作辅助线，直观明了，利用两定理作出的解答都比较理想.

这里，我们指出这两个定理的外在形式其实是统一的，即

按照上式表征的规则，这两个定理非常容易记忆和使用. 无需图示，下面仅运用向量的线性运算给出上面它们的统一证明，同时也说明：无论是空间四面体还是平面四边形，公式都是一样成立的.

证明：记A,B,C,D 为空间四面体（或平面四边形）的四个无序顶点，O 为空间（或平面）内任一点. 则

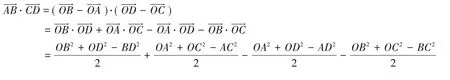
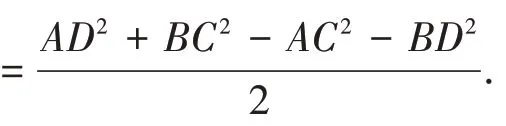
综上，通过本文给出的向量在与二面角等相关问题中的应用，可以说明运用好向量的线性运算法则，在数量积运算性质的基础上增加向量积这一工具，对求解包含二面角问题在内的空间解析几何问题与立体几何问题是有益的.