思政元素与函数曲线凹凸性教学的有机融合

闫伟杰

(浙江同济科技职业学院 基础部，浙江 杭州 311231)

习近平总书记在全国高校思想政治工作会议上指出：“要坚持把立德树人作为中心环节，把思想政治工作贯穿教育教学全过程，实现全程育人，全方位育人，努力开创我国高等教育事业发展新局面。”[1]数学问题往往来源于实际生活。正如文学家怀特所说：“数学真理既是人所发现的，又是人所创造的，它们是人类头脑的产物。”数学课程教学倘若直接导入概念，学生往往难以接受，只有将知识点与具体实际相融合，才能激发学生的积极性，也能让学生充分理解数学与生活的紧密联系，进而为学生利用数学理论服务生活打下基础。为了更好地把思政元素融入课堂[2-4]，贯彻习近平总书记讲话精神，本文结合“高等数学”课程理论性强、抽象性高、学习时间长等特点，探究函数曲线凹凸性教学与思政元素的结合点。

1 数学问题的导入

杭州湾跨海大桥已建成10年。该桥北起浙江嘉兴，南至浙江宁波，是目前世界上长度第三的跨海大桥。大桥南航道约1.7公里延伸处的“海天一洲”展望台是大桥的点睛之作。登高望远，看长桥寝波，听海潮翻滚，大桥在海面上呈优美的曲线，活泼生动，是一场震撼人心的视觉盛宴。作为世界级的工程，工程建设解决了许多棘手的技术难题。大桥建设者们获得了250多项技术革新，打破了国外的技术垄断，取得了9项核心自主创新成果，其中多项成果达到世界领先水平，为国内外同类桥梁的建设提供了宝贵经验，不仅体现了中国人民的智慧，也体现了建设者们爱岗敬业的奉献精神和精益求精的“工匠精神”。在教学过程中，教师以视频和PPT课件的方式呈现给学生，借此鼓励学生要学习建设者们难能可贵的品质， “立鸿鹄之志”“求科学真知”“练过硬本领”，将来为祖国建设贡献自己一份力量。

教师借由杭州湾跨海大桥的外形(如图1所示)，引发学生思考：按照两点之间线段最短的理论，大桥为什么没有设计成直线形，而是设计成弯弯曲曲的形态呢？在此基础上，向学生介绍一些其他学科相关知识，让学生感受到数学与其他学科的紧密联系。同时告诫学生：决定事物的成因往往不止一个，在分析问题时应该全面、透彻，要透过现象发现事物的本质。杭州湾和亚马逊河口、恒河河口并称为世界三大强潮海湾，气候环境非常复杂，经常有台风、乱流。为了减轻海潮对桥墩的冲击，减少大桥对钱塘江大潮的影响，同时借鉴西湖苏堤“长桥卧波”的理念，曲线造型比直线更具美感并且有助于车辆安全驾驶，所以杭州湾跨海大桥被设计为弯弯曲曲的形态。

图1 杭州湾跨海大桥

基于此情景，笔者设计问题[5]：现有杭州湾跨海大桥部分施工段的初步设计方案(如图2所示)由于没有充分考虑大桥的美观以及驾驶员安全行驶的问题，在连接两端曲线时，采用了直线连接的方式。现请学生对已有方案进行改进，使方案更加合理。通过创设问题，使学生充分参与到教学过程中，激发了学生的好奇心，发挥了学生的主观能动性。

图2 创设问题图

2 教学问题分析

为了解决所提出的问题，我们需要对曲线加以研究。鉴于学生已经学习过函数的特性，具备了分析函数图像的基本能力,因此，我们把函数曲线分为两类进行研究:一类开口向上(如图3所示)，另一类开口向下(如图4所示)。

图3 开口向上的曲线图

图4 开口向下的曲线图

为了更好地描述曲线的性态，我们需要引入函数图像的一个新概念：函数曲线的凹凸性。下面将通过分析弦与弧的位置关系、切线与弧的位置关系引导学生给出函数曲线凹凸性的定义以及曲线凹凸性判断的代数方法。

2.1 弦与弧的位置关系

从简单入手，通过作图让学生直观地体会到弦与弧的位置关系，启发学生思考。对于开口向上的曲线(如图5所示)，可以得出它们的相同之处在于：光滑曲线上任意两点之间的弧段总在这两点连线的下方，我们把具有这种特性的曲线称为凹的；相应的，对于开口向下的曲线(如图6所示)，不难发现，曲线上任意两点之间的弧段总在这两点连线的上方，我们把具有这种特性的曲线称为凸的。由以上分析，继续引导学生将这种通过几何直观得到的结论转化为数学语言。

图5 弦与开口向上曲线位置关系图

图6 弦与开口向下曲线位置关系图

以图5中的曲线为例，曲线上任意两点之间的弧段总在这两点连线的下方(两端点除外)，则弧的中点一定位于它所对应的弦的中点的下方，将其转化为代数关系，可以得到凹曲线的定义：

设函数f(x)为定义在区间I上的函数，若对曲线上任意两点x1、x2，总有

则称函数f(x)在区间I上的图像为凹的。相应地，给出凸曲线的定义：

设函数f(x)为定义在区间I上的函数，若对曲线上任意两点x1、x2，总有

则称函数f(x)在区间I上的图像为凸的。

不难发现，利用上述定义判断函数曲线的凹凸性比较复杂。由此继续引发学生思考：是否存在简单的判断方法？

2.2 切线与弧的位置关系

借助画图工具，作图7，启发学生观察和思考：能否利用切线与弧的关系，推出函数曲线凹凸性的判别方法？学生通过讨论，得到结论：如图7所示，对于凹曲线，其切线位于曲线的下方；对于凸曲线，其切线位于曲线的上方。通过PPT动画演示，进一步引导学生发现规律：如果曲线f(x)在(a,b)内是凹的，则切线的斜率是一个递增的函数；如果曲线f(x)在(a,b)内是凸的，则切线的斜率是一个递减的函数。因此，利用函数的二阶导可以得到如下结论：设函数f(x)在(a,b)内具有二阶导数，如果函数f(x)

(1) 在(a,b)内f″(x)>0，则曲线y=f(x)在区间(a,b)内是凹的；

(2) 在(a,b)内f″(x)<0，则曲线y=f(x)在区间(a,b)内是凸的。

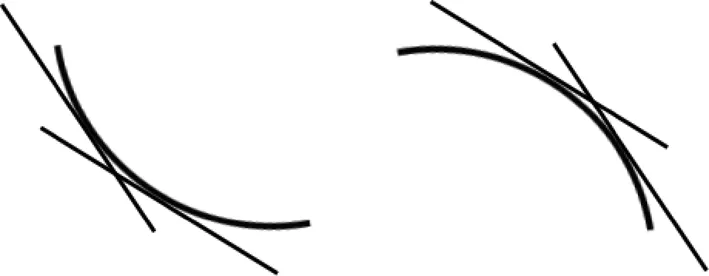
图7 切线与弧的位置关系图

通过职教云布置练习题，让学生掌握利用函数的二阶导数判断函数曲线凹凸性这种方法。同时，引导学生总结利用定义判断函数曲线凹凸性与利用函数的二阶导判断函数曲线凹凸性的利弊。最后，通过对问题的分析，让学生体会到人生哲理：遇到问题应该沉着冷静，认真思考，从已知入手，用自己的已有知识来解决问题。处理问题应该由易到难，把问题分解，各个击破，最终解决问题。

3 预设问题求解

通过问题分析，我们得到了函数曲线凹凸性的定义及其判别方法。回到开始的问题，引导学生继续思考，要想设计更为合理的方案，则需要考虑多方面因素：海洋的底部丘陵起伏、尽量减少驾驶员的疲劳感、大桥设计的美观性、海洋中的洋流和海流等[6-7]。通过分析可得，将图2中的直线部分设计为水平的光滑曲线更为合理。进一步判断可知，该水平光滑曲线的一阶导函数是单调递减的，即二阶导函数小于零。因此，我们利用函数曲线凹凸性的判别方法得出该曲线应该为凸曲线。但不同弯曲程度的凸曲线有许多种，要了解这方面知识就需要对曲率和曲率半径进行学习。

通过对问题的分析和求解，让学生体会到数学知识的完整性与系统性，体会到每一个“国之重器”的建设者都需要具备扎实的理论基础。只有努力学习，才能为实现中华民族伟大复兴贡献自己的力量。课后，教师请学生继续收集有关函数曲线凹凸性的案例，让学生深切感受到科技的发展离不开数学，培养学生们在生活中思考数学的思维。

4 结语

思政元素融入课堂，是一种全新的授课方式，需要教师不断学习与思考，采用合理的方式方法，自然地与授课内容相结合。本文首先以杭州湾跨海大桥为导入，向学生们展示国家超级工程，增强学生的民族自尊心和自豪感，激发学生的学习兴趣，提高学生学习的主动性。其次，通过创设问题，使学生充分参与到教学过程中来，激发学生的好奇心，增加师生之间的互动。再者，采用由易到难的方法，通过简单的几何模型，启发学生导出函数曲线凹凸性的定义以及判断方法，让学生体会人生哲理的同时实现教学目的。最后，通过利用所学知识解决所提出的问题，让学生体会到学习的快乐，激发学生的学习热情。

生活中有许多与函数曲线凹凸性有关的案例，比如导弹轨迹设计、高空输电线施工、高铁建设、港珠澳大桥设计等。通过数学知识的教学，使学生在学习专业知识的同时，对国家取得的举世瞩目的成就有了更深入的了解，增强了民族自信心和自豪感。

在高等数学中还有许多与思政元素结合的知识点。比如：刘徽的割圆术、罗尔定理、拉格朗日中值定理、柯西中值定理、洛必达法则、牛顿-莱布尼兹公式等。通过课程思政元素的融入，让学生感受到数学家们所取得的伟大成就，并引导学生把崇高的理想与务实精神结合起来，打好坚实基础，学好过硬本领，将来为实现人生理想不懈奋斗。此外，在极限概念的讲授中，教师还可以引入运动与静止的辩证关系思想，引导学生改变思维习惯，用动态的观念去研究世界；在定积分概念的讲授中，可以引入量变到质变的辩证关系思想，引导学生在学习上要厚积薄发，生活中要防微杜渐；在学习第二曲面积分时，可以与三峡大坝的流量问题[8]相结合，使学生感受到数学知识的实用性与无穷魅力，使学生增加对数学的热爱。