多重扭曲乘积浸入*
陈海莲,钟定兴
(赣南师范大学 a.科技学院;b.数学与计算机科学学院,江西 赣州 341000)
1 基本概念

扭曲乘积流形的定义最早出现在Bishop和O’Neill的著作中,Bishop和O’Neill利用扭曲乘积流形构造了许多负曲率流形的例子.在Bishop和O’Neill之前的数学和物理学的一些文献中也出现过扭曲乘积,只不过没有给出扭曲乘积的定义.比如,KruchKovich把扭曲乘积称为半约化空间.扭曲乘积流形与理论物理联系密切,爱因斯坦场方程和规范场方程的某些解是扭曲乘积流形.
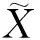
设φi:Ni→Mi是黎曼流形Ni到黎曼流形Mi的等距浸入,1≤i≤l,定义φ=(φ1,φ2,…,φl):N1×f2N2×…×flNl→M1×ρ2M2×…×ρlMl,φ(p1,p2,…,pl)=(φ1(p1),φ2(p2),…,φl(pl)),其中fi=ρi°φi,2≤i≤l.那么φ是扭曲乘积流形N1×f2N2×…×flNl到扭曲乘积流形M1×ρ2M2×…×ρlMl的等距浸入,φ称为多重扭曲乘积浸入[1].
扭曲乘积浸入出现在微分几何的某些方面的研究当中,见文献[1-4].
本文研究扭曲乘积流形到扭曲乘积流形的等距浸入的有关性质,得到了这样的等距浸入为全测地浸入,或为全脐浸入,或为极小浸入的充要条件,推广了文献[1]的相应结论.
2 主要结论及其证明
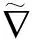
引理1设φ=(φ1,φ2,…,φl):N1×f2N2×…×flNl→M1×ρ2M2×…×ρlMl是多重扭曲乘积浸入,那么

(1)
∇XV=∇VX=(Xlnfi)V,X∈L(N1),V∈L(Ni), 2≤i≤l,
(2)
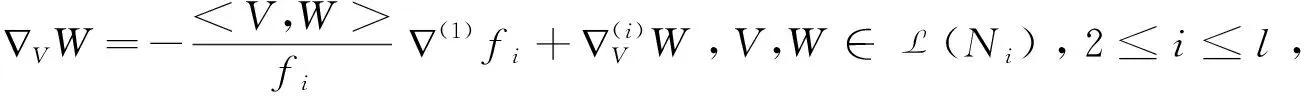
(3)
∇VU=∇UV=0,V∈L(Ni),U∈L(Nj), 2≤i,j≤l,i≠j,
(4)
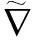
记φ和φi:Ni→Mi的第二基本形式分别是h和h(i),可得到[1]
引理2h(X,Y)=h(1)(X,Y),X,Y∈L(N1),
(5)
h(X,V)=0,X∈L(N1),V∈L(Ni),i≥2,
(6)
h(V,W)=h(i)(V,W)-
(7)
h(V,U)=0,V∈L(Ni),U∈L(Nj),i,j≥2,i≠j
(8)
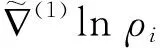
利用引理1和引理2,首先考虑扭曲乘积浸入是全测地的条件.
定理1设φ是一个多重扭曲乘积浸入,那么
证明设X∈L(N1),V∈L(Ni),W∈L(Nj), 2≤i,j≤l,i≠j,由引理2可得
h(X,V)=0,h(V,W)=0,
(9)
所以φ是混合全测地的.
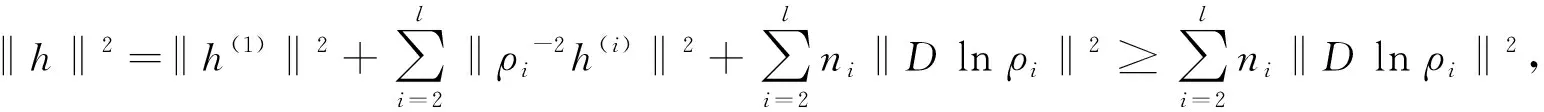
(10)
等号成立当且仅当h(i)=0,1≤i≤l.即φi:Ni→Mi都是全测地的,1≤i≤l.
下面考虑多重扭曲乘积浸入是全脐的条件.
定理2多重扭曲乘积φ=(φ1,φ2,…,φl):N1×f2N2×…×flNl→M1×ρ2M2×…×ρlMl是全脐的当且仅当以下2个条件同时成立:
证明设多重扭曲乘积浸入φ是全脐的,那么

(11)
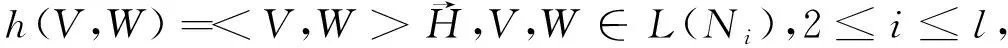
(12)


(13)
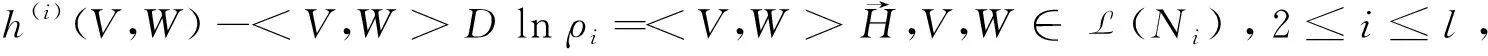
(14)
h(i)(V,W)=0,V,W∈L(Ni),2≤i≤l
(15)
即对2≤i≤l,φi:Ni→Mi都是全测地.把(15)代入(14),可得
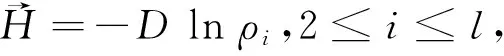
(16)
由(13)(16)可得
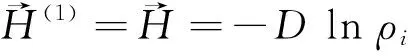
(17)

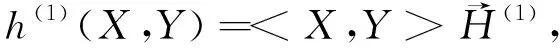
(18)
因此φ1:N1→M1是全脐的,且φ1的平均曲率向量是-Dlnρi,2≤i≤l.
h(1)(X,Y)=
(19)
h(i)(V,W)=0,V,W∈L(Ni),i≥2.
(20)
由引理2可得
h(X,Y)=
(21)
h(V,W)=-
(22)
由(21)可得
Dlnρ2=Dlnρ3=…=Dlnρl.
(23)
由(21)-(23)可得
H=-Dlnρi.
(24)
因此
h(X,Y)=
(25)
h(V,W)=
(26)
对于N1×f2N2×…×flNl上的任意向量场X=X1+X2+…+Xl,Y=Y1+Y2+…+Yl,其中Xi,Yi∈L(Ni),由引理2有
h(X,Y)=h(X1,Y1)+h(X2,Y2)+…+h(Xl,Yl)=
(
(27)
所以φ全脐的.证毕.
注定理2是文献[1]中定理2的推广.
最后考虑极小多重扭曲乘积浸入.
定理3设φ是多重扭曲乘积浸入,那么
证明在N1×f2N2×…×flNl上取标准正交基e1,e2,…en1,…,etl-1+1,…,etl-1+nl,其中eti-1+1,…,eti-1+ni是Ni上关于Ni上的黎曼度量gi的标准正交基的提升的倍,f1=1,ti=n1+n2+…+ni,t0=0,0≤i≤l-1,因此,由(5)得
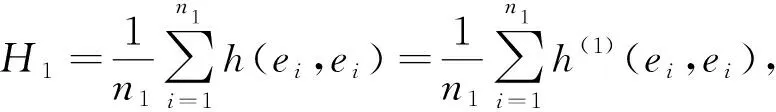
(28)
所以φ的部分平均曲率向量H1等于φ1:N1→M1的平均曲率向量,φ是N1极小当且仅当φ1是极小的.
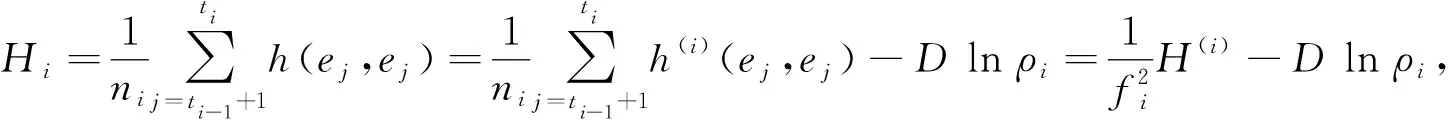
(29)
这里H(i)是φi:Ni→Mi的平均曲率向量,注意到Dlnρi是M1上的向量场,H(i)是Mi上的向量场,故Dlnρi与H(i)是正交的.所以φ是Ni极小的当且仅当
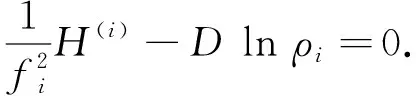
(30)
即H(i)=0,且-Dlnρi=0,也就是φi:Ni→Mi是极小的,且Dlnρi=0.
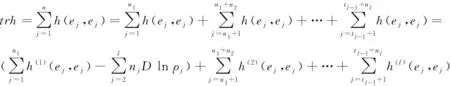
(31)
最后一个等式右边的第1,2,…,l项分别是M1,M2,…,Ml的向量场,所以φ是极小的充分必要条件是

注定理3是文献[1]中定理3的推广.

