具有恐惧和强Allee效应的离散食饵-捕食者模型
胡新利,李航航
(西安工程大学 理学院,陕西 西安 710048)
0 引 言
在种群系统中,群聚有利于种群的增长和生存,但种群数量过大或过小将会阻碍其发展,最终会导致种群趋于灭绝,这就是Allee效应[1]。食饵-捕食者模型是基本的种群模型之一,许多学者建立了各类食饵-捕食者模型,并对其进行动力学分析。捕食者除了直接捕杀食饵之外,还会对食饵的觅食、防御和繁殖等行为产生影响,为此,WANG等首次提出具有恐惧效应的食饵-捕食者模型[2],并引起了众多学者的广泛关注[3-5]。
在种群动力学中,连续或离散模型是描述种群数量变化的2种常用形式。众多研究表明[6-7]:当种群具有不重叠的世代时,由差分方程描述的离散模型比连续模型更贴近实际。ZHU[8]和CUI[9]等分别研究了具有Holling Ⅳ功能反应的连续和离散Lotka-Volterra食饵-捕食者模型的定性行为。相比而言,离散系统要比连续系统具有更丰富的动力学行为,能够产生倍周期分支、Neimark-Sacker分支、混沌和更复杂的动力学行为。KUNDU等研究了恐惧效应在具有线性功能反应的离散食饵-捕食者模型中的影响,并对该模型进行了稳定性分析和分支分析[10]。BANERJEE等研究了具有恐惧效应和Holling Ⅲ型功能反应的离散时滞双食饵-捕食者模型,得到了平衡点存在的条件,并给出了正平衡点的持久性和全局稳定性的充分必要条件[11]。文献[12]研究了具有恐惧效应的离散捕食者-食饵模型,并对其进行了稳定性分析,获得了在正平衡点处发生倍周期分支的条件。CELIK[13]等和DIN[14]分别使用不同的离散方式研究了具有Allee效应的食饵-捕食者模型的分支分析。
1 模型的建立
有研究表明,除了直接捕杀之外,对捕食者产生的恐惧会使食饵的增长率降低40%。因此,文献[15]提出了一类具有恐惧效应和强Allee效应的连续食饵-捕食者模型,考虑了在繁殖过程中,食饵已经受到交配诱导的强Allee效应的影响,并考虑了由于对捕食者的恐惧而使食饵的生长速度降低,具体模型如下:
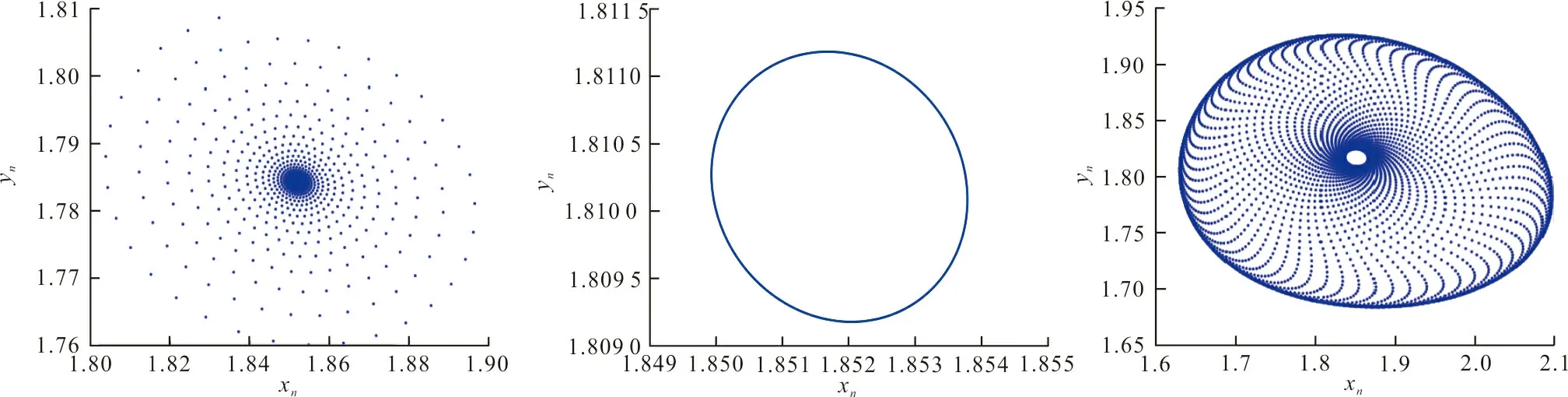
式中:r、A、f、K、b、β和d均为正常数;r为食饵种群的内禀增长率;A为食饵种群灭绝的Allee阈值(0 文献[15]主要讨论了系统(1)所有平衡点的稳定性条件,并分析了系统(1)在平衡点处发生Hopf分支。但对于离散系统会产生更丰富的动力学行为,为此,对系统(1)进行离散化。为了避免离散系统存在负解,利用文献[16]中的分段常数变元的方法,得到连续系统(1)对应的离散系统 式中:xn和yn分别是食饵和捕食者在n世代的种群密度,其他参数同系统(1)。类似的离散化方式参见文献[17-18]。 系统(2)的平衡点可以通过代数方程 求得。通过求解方程(3),可以得到如下定理。 定理1 系统(2)有以下4个平衡点。 1) 食饵和捕食者均灭绝的平衡点E0(0,0)。 2) 食饵存在捕食者灭绝的平衡点E1(K,0),E2(A,0)。 a21=bβyexp(bβx-d),a22=exp(bβx-d)。 定义1[19]平衡点E(x,y)处的雅可比矩阵J(x,y)对应的特征方程为 λ2-trJ(x,y)λ+detJ(x,y)=0 (4) 令λ1和λ2是上述方程(4)的2个根,有: 1) 若|λ1|<1且|λ2|<1,则E(x,y)是汇且局部渐近稳定; 2) 若|λ1|<1且|λ2|>1(或|λ1|>1且|λ2|<1),则E(x,y)是鞍点且不稳定; 3) 若|λ1|>1且|λ2|>1,则E(x,y)是源且不稳定; 4) 若|λ1|=1或|λ2|=1,则E(x,y)是非双曲的。 通过简单计算,系统(2)在平衡点E0(0,0)、E1(K,0)和E2(A,0)处的雅可比矩阵对应的特征方程的根分别为: 1)λ1=exp(-rA),λ2=exp(-d); 因此,可以得到如下定理。 定理2 1) 系统(2)的平衡点E0(0,0)是汇且局部渐近稳定。 2) 系统(2)的平衡点E1(K,0)具有以下性质: 3) 系统(2)的平衡点E2(A,0)具有以下性质: 为了考虑系统(2)唯一正平衡点E3(x*,y*)的稳定性,需要引进以下引理。 引理1[20]考虑二次特征多项式 F(λ)=λ2-α1λ+α2 式中:α1和α2为实系数。因此,特征多项式对应的特征方程的2个特征根都位于开的单位圆盘内的充分必要条件为|α1|<1+α2<2。 P(λ)=λ2-trJλ+detJ (5) 其中, 应用引理1得到如下定理。 当特征多项式(5)对应特征方程的特征值是一对模为1的复共轭根,则系统(2)在唯一正平衡点E3(x*,y*)处会产生一个Neimark-Sacker分支,且此条件可以写成集合形式,即 ΩNS={(A,f,b,β,d,r,K):(trJ)2- 4detJ<0,detJ=1}。 现在讨论系统(2)的所有参数在集合ΩNS的小邻域内变化时,在唯一正平衡点E3(x*,y*)处发生的Neimark-Sacker分支。 其中|K*|≪1表示小的扰动参数。令x=X-x*,y=Y-y*,则映射方程(7)转化为 其中: g1(x,y)=a13x2+a14xy+a15y2+b1x3+ b2x2y+b3xy2+b4y3+O((|x|+|y|)4) g2(x,y)=a23x2+a24xy+d1x3+ d2x2y+O((|x|+|y|)4)。 λ2-T(K*)λ+D(K*)=0 (9) 其中: 因此,可以得到: 假设T(0)≠0,1,即 并且考虑下面的变换 在式(10)的转换下,线性化系统(8)的标准形式可以写为 其中: O((|u|+|v|)4)。 式中:x=a11u;y=(φ-a11)u-ψv。定义非零实数 其中: 例1 设系统(2)中的参数值为r=0.78,A=0.15,f=0.7,b=0.12,β=0.46,d=0.1,K=3.2且初始值x0=1.81,y0=1.96。 系统(2)在唯一正平衡点E3(x*,y*)处雅可比矩阵对应的特征多项式为P(λ)=λ2-1.949 3λ+0.986 6,则|1.949 3|<1+0.986 6<2。 因此,系统(2)在唯一正平衡点E3(1.811 6,1.969 8)是局部渐近稳定的(定理3),如图1所示。 (a) 系统(2)的xn图 (b) 系统(2)的yn图 (c) 系统(2)的相图图1 系统(2)唯一正平衡点E3的局部渐近稳定性Fig.1 The local asymptotic stability diagram of the unique positive equilibrium point E3 of system (2) 例2 设系统(2)中的参数值为r=0.75,A=0.11,f=0.94,b=0.12,β=0.45,d=0.1,3 λ2-1.964 596 587 250 718λ+1=0 (12) 此外,特征方程(12)的根为: λ1=0.982 3+0.187 3i, λ2=0.982 3-0.187 3i。 且|λ1,2|=1。因此, (r,A,f,b,β,d,K)= (0.75,0.11,0.94,0.12,0.45,0.1,3.362 17)∈ΩNS。 系统(2)发生的分支图和最大Lyapunov指数图如图2所示。 (a) xn的分支图 (b) yn的分支图 (c) 最大Lyapunov指数图图2 系统(2)分支图和最大Lyapunov指数Fig.2 Bifurcation diagram and maximum Lyapunov exponents of system(2) 从图2可以看出:当K 分支参数在K∈[3,4.2]内变化时的相图见图3。当K=3.3时,平衡点E3(1.851 9,1.784 4)是局部渐近稳定的,见图3(a)。当K=3.3 时,形成光滑的闭合不变曲线,见图3(b)。图3(c)、(d)表明这些闭合不变曲线的半径随着K的增大而增大。此外,当K=4 时,闭合不变曲线消失,见图3(e),产生混沌吸引子,见图3(f)。 (a) K=3.3 (b) K=3.362 17 (c) K=3.38 对具有恐惧效应和强Allee效应的离散食饵-捕食者模型进行动力学分析。相比连续系统能够发生Hopf分支之外,离散系统具有更丰富的动力学性质。以K作为分支参数,系统能够在正平衡点处发生Neimark-Sacker分支和更复杂的动力学行为,使得捕食者和食饵种群的稳定性发生改变,最终可能导致种群之间过度拥挤或者完全崩溃。从数值模拟可以直观地看出系统正平衡点的局部渐近稳定性、Neimark-Sacker分支等丰富的动力学行为。2 平衡点的存在性和稳定性

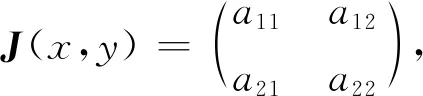
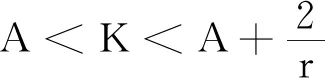
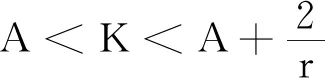

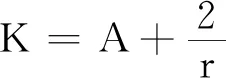
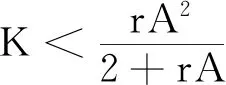
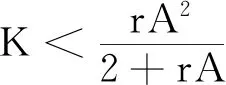
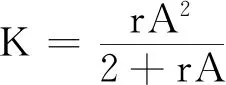


3 Neimark-Sacker分支

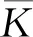
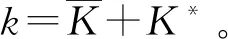



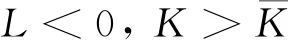
4 数值模拟


5 结 语

