基于逆向设计理论的高中数学教学
【摘 要】逆向设计是一种先确定学习的预期结果,再明确预期结果达到的条件,最后设计教学活动的教学设计模式。教师利用逆向设计理论设计教学,能够促进学生自主有效学习,落实数学核心素养的培养要求。
【关键词】高中数学;逆向设计;函数的零点;教学实践
【中图分类号】G633.6 【文献标志码】A 【文章编号】1005-6009(2024)07-0055-04
【作者简介】周星月,南京市中华中学(南京,210019)教师,一级教师。
一、逆向设计理论概述
逆向设计是一种以学习目标为起点,教学评价设计先于教学活动设计,指向目标达成的教学设计模式。其主要有三个阶段:阶段一,明确预期的学习结果,即确定学习目标;阶段二,确定合适的评估证据,即设计教学评价;阶段三,设计教学活动。逆向设计与传统教学设计最大的不同在于:“学习评价”在先,“教学活动”在后,利用“评价优先”将学生评价纳入教学活动中,关注学生需要什么及如何获得,有利于学生生成可供后续发展的深层次理解。
下面笔者以苏教版高中数学必修一“函数的零点”教学为例,阐述如何将逆向设计理论应用于高中数学教学实践。
二、逆向设计理论下的“函数的零点”教学设计与实践
(一)学习目标设计
逆向设计理论强调以预期结果为导向,在教学设计之初,教师要先依据课标要求、学生学情和教材内容确定学习目标。
1.教学内容分析
“函数的零点”作为函数应用的开篇,从不同的角度将数与形、函数与方程联系在一起。《普通高中数学课程标准(2017年版2020年修订)》(以下简称“新课标”)将“从函数观点看一元二次方程和一元二次不等式”作为主题一“预备知识”的一个单元,借助一元二次函数的图象,让学生了解一元二次不等式与相应函数、方程的联系。本节课是在此基础上,对一般函数零点的整体性的认识,同时为后续“二分法求方程的近似解”的学习提供认知基础。
2.学情分析
授课对象为江苏省四星级普通高中学生,学生学习数学的基础扎实、兴趣浓厚。根据教材安排,学生已经学习了二次函数的零点与方程根的关系,又经历了函数概念及其性质、基本初等函数的学习,具备一定的用数形结合思想解决问题的能力。但高一学生仍处于经验性逻辑思维阶段,从直观到抽象的概括归纳能力较弱,自觉运用数形结合思想解决问题的意识不强,因而自主探究发现函数零点存在的判定方法并归纳总结出函数零点存在定理相对较难。
3.学习目标设置
逆向设计理论下的教学,通常从行为主体、行为动词(了解、理解、掌握)、行为条件和表现程度四个方面设置学习目标,让学习者知道“学什么”“能做什么”“需要发展什么”。本节课学习目标如下:
(1)通过对二次函数零点概念的复习,掌握一般函数零点的定义,了解一般函数的零点、方程的根与图象交点之间的联系,能够进行简单的函數与方程的相互转化。
(2)通过对特殊函数的研究,探究零点存在定理条件,归纳出一般函数的零点存在性分析方法,体会从特殊到一般的数学研究思路,激发学生的探究兴趣和求知欲,提升其数学抽象和直观想象素养。
(3)通过概念辨析,体会零点存在定理条件的完备性和定理的不可逆性,培养学生的批判性思维能力;通过例题练习巩固用零点存在定理对一般函数的零点情况的定性判断方法,提升学生的数学运算素养。
(二)教学评价设计
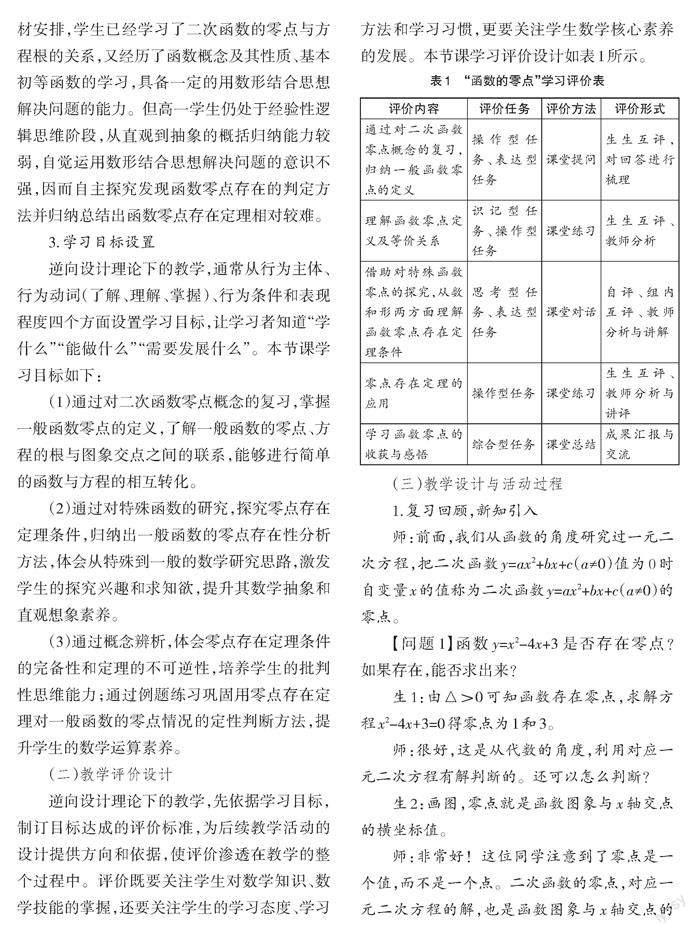
逆向设计理论下的教学,先依据学习目标,制订目标达成的评价标准,为后续教学活动的设计提供方向和依据,使评价渗透在教学的整个过程中。评价既要关注学生对数学知识、数学技能的掌握,还要关注学生的学习态度、学习方法和学习习惯,更要关注学生数学核心素养的发展。本节课学习评价设计如表1所示。
(三)教学设计与活动过程
1.复习回顾,新知引入
师:前面,我们从函数的角度研究过一元二次方程,把二次函数y=ax2+bx+c(a≠0)值为0时自变量x的值称为二次函数y=ax2+bx+c(a≠0)的零点。
【问题1】函数y=x2-4x+3是否存在零点?如果存在,能否求出来?
生1:由△>0可知函数存在零点,求解方程x2-4x+3=0得零点为1和3。
师:很好,这是从代数的角度,利用对应一元二次方程有解判断的。还可以怎么判断?
生2:画图,零点就是函数图象与x轴交点的横坐标值。
师:非常好!这位同学注意到了零点是一个值,而不是一个点。二次函数的零点,对应一元二次方程的解,也是函数图象与x轴交点的横坐标值。函数不只有二次函数,那么如何定义一般函数y=f(x)的零点?
教师给出零点的定义:一般,我们把使函数y=f(x)的值为0的实数x称为函数y=f(x)的零点。
【设计意图】教学从一个具体的二次函数入手,引导学生从数、形两方面认识函数零点,归纳得到:方程f(x)=0有解?函数y=f(x)有零点?函数y=f(x)的图象与x轴有交点。
2.探究归纳,概念生成
【问题2】以下函数是否存在零点,你是如何判断的?①f(x)=lnx+2x-6;②f(x)=x3-4x+1。
生3:因为y=lnx与y=6-2x图象有交点,所以函数①有零点。
师:你怎么想到这么做的?
生3:函数有零点,等价转化为方程lnx=6-2x有解,再转化为两函数图象有交点。
师:非常好,将陌生的问题转化为熟悉的函数问题,数形结合,利用图象直观判断出有零点。那函数②呢?
生3:因为f(1)<0,f(2)>0,所以我判断函数有零点。
师:为什么没像函数①那样画图判断了呢?
生3:y=x3图象画出后,我不是很确定与直线y=4x-1有没有交点,就想找其他办法。
师:很好,函数①借助“形”足以直观判断零点存在,但当几何直观不够精确时,要学会从代数角度寻找判断零点存在的条件。那函数②零点所在区间是什么呢?
生3:(1,2)。
师:其他同学赞同他的结论吗?
生4:我认为要加上一个条件——函数在[1,2]连续,否则函数不一定有零点。
师:你能举例说明吗?
学生板书画出满足f(1)<0,f(2)>0,但函数图象在[1,2]断开的分段函数图象。
师:非常棒,看来需要加上函数在[1,2]上图象不间断。函数①也能用函数值判断零点是否存在吗?
生5:可以。因为f(1)<0,f(3)>0,函数f(x)=lnx+2x-6在[1,3]图象不间断,所以存在零点。
师:很好,但是老师刚才看到有同学写“f(x)在[1,3]单调递增”你认为用哪个合适?
生5:单调不行,图象可能断开。
师:非常棒!你们不仅判断出了函数有零点,更进一步给出了零点的范围。你们能否推广到一般,给出函数y=f(x)在区间(a,b)上有零点的条件呢?
生6:若函数y=f(x)在区间(a,b)上的图象不间断,且f(a)f(b)<0,则函数y=f(x)在区间(a,b)上有零点。
师:其他同学赞同吗?
生7:我认为要改成函数y=f(x)在区间[a,b]上图象不间断,否则图象可能在区间端点断开。
学生板书画图举反例,强化条件中应是“闭区间[a,b]”,同时辨析结论中要用“开区间(a,b)”。
师:什么叫“有”零点,有几个?
生众:至少一个。
师:能举出不止一个的例子吗?
学生画图。
追问1:对于一般函数,能否加一个条件,使零点唯一?
追问2:是否一定要单调?能举例吗?
【问题3】判断以下命题是否正确:若函数y=f(x)在区间[a,b]上的图象是一条不间断的曲线,且f(a)f(b)>0,则函数y=f(x)在区间(a,b)上没有零点。
学生画出满足条件的二次函数图象作为反例,论证上述命题错误。
追问:闭区间[a,b]上的连续函数y=f(x),f(a)f(b)<0是函数y=f(x)在区间(a,b)上有零点的 条件。
【设计意图】教学从具体的函数存在零点条件的讨论开始,通过师生对话、生生对话,让学生充分经历零点存在定理的生成过程,自主探究归纳出零点存在定理。教学中反复从“数”“形”角度认识函数的零点问题,使学生最终从数、形两方面获得对零点存在定理的全面理解,培养学生的理性思维、辩证思维、分析和解决问题的能力、创新意识和探究能力。
3.例题精讲,知识应用
师:函数①有几个零点?如何判断?
生众:一个零点,因为函数①单调。
师:函数②呢?如何判断?
生8:对应三次方程x3-4x+1=0,我觉得函数有三个零点。
教师用GeoGebra软件展示函数f(x)=x3-4x+1的图象,请学生板书证明函数f(x)=x3-4x+1在区间(-3,-2)上有零点。
例1:求证函数f(x)=2x+2x-3有零点。
【设计意图】上述教学旨在培养学生学会利用零点存在定理证明函数有零点。教师通过请学生板书,规范学生解答过程。同时,教师追问:如何缩小零点范围?留待课后思考,为下节课“二分法”的学习埋下伏笔。
4.归纳总结,练习巩固
课堂小结:今天这节课你有什么收获?
【设计意图】教师引导学生从知识(函数零点和函数零点存在定理)和思想方法(特殊到一般、函数与方程、数形结合、转化化归)两方面进行课堂小结。
三、教学反思
新课标指出,高中数学课程以学生发展为本,落实立德树人根本任务,提升数学学科核心素养。新课标对学生数学素养提出的要求,也是对教师在教学上的要求,创新教学手段、改革学生评价方式、变革教学组织形式,自然成为应有之义。逆向设计正是顺应新课程改革和新高考形势,指向数学核心素养提升的一种教学设计形式,其特点主要体现在以下几方面。
(一)立足学情,以学习目标落实课标要求
“逆向设计”在教学设计之初,就依据学生实际将上位的课程目标转化为针对性强、可操作的课时学习目标,实现由基于经验的教学向基于课程标准的教学的转变,增强教学的指向性。在分析学情时,不仅考虑学生已有的知识和能力基础、惯用的思维方式等智力因素,同时兼顾学习态度、学习习惯、学习兴趣等非智力因素。在上述教学中,教师统观“函数的应用”此章大单元教学要求,把握新课标要求与学生已有基础的落差,剖析函数零点的概念形成及零点存在定理的生成过程中分别体现的数学核心素养,在学生的最近发展区内设计学习目标,帮助学生形成可供后续发展的深层次理解,促进他们数学核心素养的发展。
(二)注重过程,以学习评价促进学习效果
传统教学设计将评价设计放在教学活动设计之后,甚至不出现在教学设计文案中,常只以终结性评价检测学生的掌握情况,忽视了评价的诊断和促进作用。而“逆向设计”的评价设计先于教学活动,先确定目标达成的证据,进而判断学生已有学习经验和目标的距离,再根据证据的需要设计教学活动。上述教学设计借助学生已知的二次函数零点,将一般函数零点的概念纳入到学生原有的知识体系。问题2的探究过程中,以教师、学生本人以及同学作为评价主体,以课堂评价为主要形式,让评价贯穿整个教学过程,真实反映了学生认知和思维的发展,帮助教师及时监控学习目标的达成情况,反思、调整教学行为,提高教学质量。
(三)动态调整,不断完善教学评系统
教学设计的有效性最终取决于学生学习的成果,而教学中学情常常不能直接朝着理想状态发展,学习目标的达成可能出现参差不齐、停滞、反复的情况,因而“逆向设计”也并非是一種线性的过程,而是一个循环往复、不断调整和完善的过程。在逆向设计理论中,目标指导评价和教学互动,评价是判断目标是否落实的标准,活动是评价进行的载体,三者相互制约,彼此联动。因此,教师应该根据教学实际情况调整和修改三个环节,以保证教学的各要素协调一致、前后连贯,尤其是教学活动既要和评价保持一致,又要符合教学目标的要求。
【参考文献】
[1]威金斯,麦克泰.追求理解的教学设计(第二版)[M].闫寒冰,宋雪莲,译.上海:华东师范大学出版社,2017.
[2]卢卫忠,林敏.中学地理逆向教学设计策略探讨[J].中学地理教学参考,2017(23):26-29.
[3]胡革新,谢春蛾.高中数学“优效课堂”要为核心素养而教——以“方程的根与函数的零点”为例[J].中学数学教学参考,2018(13):18-21.

